NEW! The Gist (FREE) | E-BOOKS |
(IGP) IAS Pre Paper - 2: GS - Basic Numeracy - Basic Algebra
Basic Numeracy
Basic Algebra
A Civil Servant should be well-versed in basics of Algebra. In the Civil Services Aptitude Test Paper 2, in Basic Numeracy, certainly there will be asked some questions based on equations and their roots.
Polynomials
Polynomial
An expression in term of some variable(s) is called a polynomial. For example
f(x) = 2x – 5 is a polynomial in variable x
g(y) = 5y2 – 3y + 4 is a polynomial in variable y
Note that the expressions like
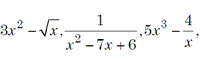 etc. are not polynomials. Thus, a rational x integral function of ‘x’ is said to
be a polynomial, if the powers of ‘x’ in the terms of the polynomial are neither
fractions nor negative. Thus, an expression of the form f(x) = an xn
+ an-1 xn-1 + …+a1x+ a0 is
called a polynomial in variable x where n be a positive integer and a0,
a1,...,an be constants (real numbers).
etc. are not polynomials. Thus, a rational x integral function of ‘x’ is said to
be a polynomial, if the powers of ‘x’ in the terms of the polynomial are neither
fractions nor negative. Thus, an expression of the form f(x) = an xn
+ an-1 xn-1 + …+a1x+ a0 is
called a polynomial in variable x where n be a positive integer and a0,
a1,...,an be constants (real numbers).
Degree of a Polynomial
The exponent of the highest degree term in a polynomial is known as its degree. For example

Linear Polynomial
A polynomial of degree one is called a linear polynomials. In general f(x) = ax + b, where a ¹ 0 is a linear polynomial.
For example
f(x) = 3x – 7 is a binomial as it contains two terms.
g(y) = 8y is a monomial as it contains only one terms.
Quadrat ic Polynomials
A polynomial of degree two is called a quadratic polynomials. In general f(x)
= ax2 + bx + c, where a ¹ 0 is a quadratic polynomial.
For example
f(x) = x2– 7x + 8 is a trinomial as it contains 3 terms
g(y) = 5x2 – 2x is a binomial as it contains 2 terms
p(u) = 9x2 is a monomial as it contains only 1 term
Cubic Polynomial
A polynomial of degree 3 is called a cubic plynomial in general. f(x) = ax3 +
bx3 + cx + d, a ¹ 0 is a cubic polynomial.
For example f(x) = 2x3 – x2 + 8x + 4
Biquadrat ic Polynomial
A fourth degree polynomial is called a biquadratic polynomial in general. f(x) = ax4 + bx3 + cx2+ dx + e, a ¹ 0 is a bi quadratic polynomial. Zero of a Polynomial A real number a is a zero (or root) of a polynomial f(x), if f (a) = 0
For example If x = 1 is a root of the polynomial 3x3 – 2x2
+ x – 2, then f(l)= 0 f(x) = 3x3 – 2x2+ x – 2, f(1) = 3 ×
13 – 2 × 12 + 1 – 2 = 3 – 2 + 1 – 2 = 0, As f 1) = 0 x = 1 is a root of
polynomial f(x)
(1) A polynomial of degree n has n roots.
(2) A linear polynomial of f(x) = ax + b, a ≠
0 has a unique root given by x = - b/a
(3) Every real number is a root of the zero polynomial.
(4) A non-zero constant polynomial has no root.
Remainder Theorem
Let f(x) be a polynomial of a degree greater than or equal to one and a be
any real number, if f(x) is divisible by (x – a), then the remainder is equal to
f(a) .
Example 1: Find the remainder when f(x) = 2x3 – 13x2
+ 17x + 10 is divided by x – 2.
Solution. When f(x)is divided by x – 2, then remainder is given by f(2) =
2(2)3 – 13 2)2 + 17(2) + 10 = 16 – 52 + 34 + 10 = 8
Thus, on dividing f(x) = 22 – 13x2 + 17x + 10 by x – 2, we get the
remainder 8.
Factor Theorem
Let f(x) be a polynomial of degree greater than or equal to one and a be any real number such that f(a) = 0, then (x – a) is a factor of f(x). Conversely, if (x – a) is a factor of f(x), then f(a) = 0. Example 2: Show that x + 2 is a factor of the polygonal x2 + 4x + 4. Solution. Let f(x) = x2 + 4x + 4 (x + 2) = {x – (–2)} is a factor of f(x) if f(–2) = 0 Now,f(–2) = (–2)2 + 4(–2) + 4 = 4 – 8 + 4 = 0 Hence, x + 2, is a factor of f(x).
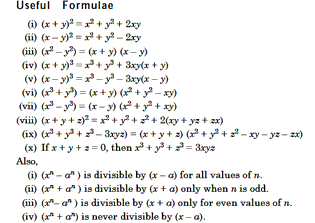
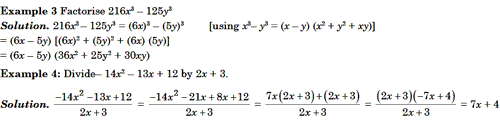
Maximum and Minimum Value of a Polynomial
Let f(x) be a polynomial. Then, f(x) has locally maxima of minima values at
a, if f(a) = 0.
If f(a) > 0, then f(x) has minimum value at x = a.
If f(a) < 0, then f(x) has maximum value at x = a.
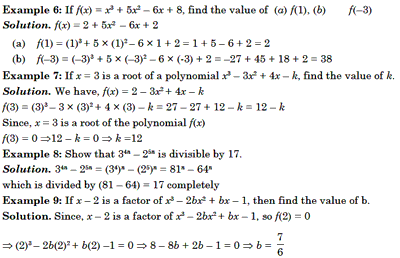

LINEAR EQUATIONS
Equations
When we equate two algebraic expressions using the sign of equality it forms an equation. Linear equation are first degree equations and may contain one or more variables. If the equation has only one variable then equation itself is sufficient to obtain the value of the variable. If the equation has two variables, then consistent equations are required to get the value of the variables. In general an equation has n variables, then n consistent equations are required to obtain all the value of the n variables.
Linear equat ions in one variable
These are first degree equations in one unknown. An equation of the form ax +
b = 0 where a, b Î R and a¹ 0 and x is the variable, is called a linear equation
in one variable.We have, only one variable x whose value have to find out.
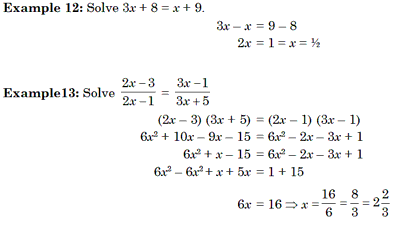
Linear Equat ions in two variables
These are first degree equations in two unknowns. An equation of the form ax + by + c = 0, where a, b, c Î R and a ¹ 0, b ¹ 0 and x, y are variables is called linear equation in two variables. We have, two variables x and y whose values we have to find out. Any pair of values of x and y which satisfy the equations ax + by + c = 0, is called its solution. When two or more equations are satisfied by the same set of values of the variables involved in them, then they are termed as simultaneous equations.
Example 14 Solve x + 2y = 7, x – y =1.
Solution. x + 2y = 7 ...(i)
x – y = 1 ...(ii)
Multiplying Eq. (ii) by 2 and adding to Eq. (i), we get
x + 2y = 7
2x – 2y = 2
3x = 9 Þ x = 3
Substituting the value of x in Eq. (ii), we get
3 – y = 1Þ y = 1 – 3 Þ 2
= y = 2
Hence, the solution is x = 3, y = 2
Consistency of a System of Linear Equations
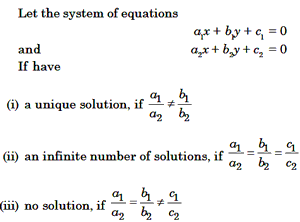
Example 16: Find the value of m for which the system of linear
equation x + 2y – 3 = 0, 5x + my + 7 = 0 have
(a) a unique solution
(b) no solution
(c) infinite number of solution
Solution. We have, x + 2y –3 =0 and 5x + my + 7 = 0
Here, al = 1, bl = 2, cl = –3,
a2 = 5, b2 = m, c2 = 7
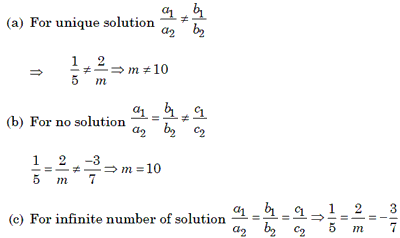
THEORY OF EQUATION
Quadratic Equation
These are second degree equations of the form ax2 + bx + c = 0, where a, b, c Î R and a ≠ 0 are quadratic equations. Like a first degree equation in x has one value of x satisfying the equation, a quadratic equation in x will have two values of x that satisfy the equation. The value of x that satisfy the equation are called the roots of the equation. These roots may be real or imaginary.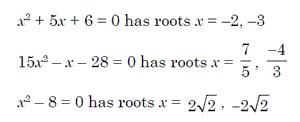
To Find the Roots of Quadrat ic Equat ion
In general, the roots of quadratic equation can be found out in two ways.
Method 1: By Factorisation
If the quadratic equation ax2 + bx + c = 0 can be expressed in the form (x – a) (x – b) = 0, then the roots of the equation are a and b.
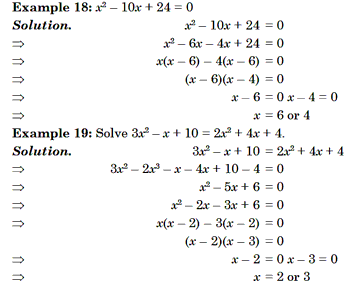
Method 2 : Using Formula
If the quadratic equation is ax2 + bx + c = 0, then we can use the standard formula given below to find out the roots of the equation. if a and b are the roots of the quadratic equation, then
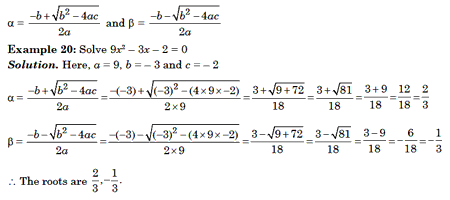

Construct ing a Quadratic Equation
If the roots of the quadratic equation are given as a and b, the equation can be written as (x – a) (x – b) = 0, ie, x2 – x (a+ b) + ab = 0. So, if we know the sum of the roots and the product of roots, we can frame the quadratic equation as x2 – x (sum of the roots) + product of the roots = 0
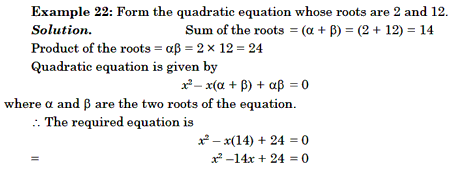
Nature of the Roots
The discriminate given by b2– 4ac determines the nature of roots of
the quadratic equation ax2+ bx + c = 0. It is represented as D.(i) If b2 – 4ac > 0 and is a perfect square, then the roots are real, rational and unequal.
(ii) If b2 – 4ac > 0 and is not a perfect square, then the root are real, irrational and unequal.
(iii) If b2 – 4ac = 0, then the roots are real, rational and equal.
(iv) If b2 – 4ac < 0, then the roots are distinct conjugate complex number or imaginary.
Example 23: Discuss the nature of the roots of the equation x2 – 6x + 9 = 0.
Solution. a = 1,b = –6 and c = 9 D = b2 – 4ac = (–6)2 –4(l)(9) = 36 – 36 = 0 Since, D = 0 the roots are real, rational and equal. Example 24: Discuss the nature of the roots of the equation 4x2 – 6x – 2 = 0. Solution. a = 4, b = –6 and c = –2
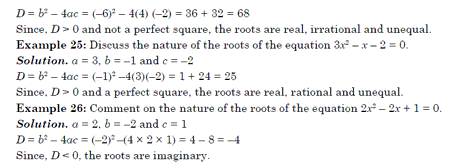
Maximum or Minimum Value of a Quadratic Expression
For the quadratic expression ax2 + bx + c
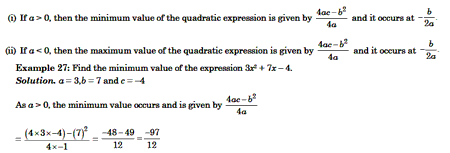
© UPSCPORTAL.COM

