Arithmetic Progression (AP)

An arithmetic progression is a sequence in which terms increase or decrease by a constant number called the common difference.
(i) The sequence 2, 6, 10, 14, 18, 22… is an arithmetic progression whose first term is 2 and common difference 4.
(ii) The sequence ..... is an arithmetic progression whose first term is 2 and common difference ½.
An arithmetic progression is represented by a,(a + d), (a + 2d), (a + 3d) a + (n – 1)d
Here, a = first term
d = common difference
n = number of terms in the progression

• The general term of an arithmetic progression is given by Tn = a + (n - 1) d.
• The sum of n terms of an arithmetic progression is given by S, = 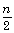[2a + (n – 1) d] or Sn = 2 [a + l]
  where l is the last term of arithmetic progression.
• If three numbers are in arithmetic progression, the middle number is called the arithmetic mean of the other two terms.
• If a, b, c are in arithmetic progression, then b = 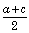where b is the arithmetic mean.
• Similarly, if ‘n’ terms al, a2, a3… an are in AP, then the arithmetic mean of these ‘n’ terms is given by
  AM =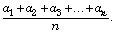
• If the same quantity is added or multiplied to each term of an AP, then the resulting series is also an AP.
• If three terms are in AP, then they can be taken as (a – d), a, (a + d).
• If four terms are in AP, then they can be taken as (a – 3d), (a – d), (a + d), (a + 3d).
• If five terms are in AP, then they can be taken as (a – 2d), (a – d), a, (a + d), (a + 2d).

Geometric Progression (GP)

A geometric progression is a sequence in which terms increase or decrease by a constant ratio called the common ratio.
(i) The sequence 1, 3, 9, 27, 81…is a geometric progression whose first term is 1 and common ratio 3.
(ii) The sequence is a geometric progression whose first term is 1 and common ratio
A geometric progression is represented by a, ar, ar2…arn–1.
Here, a = first term
r = common ratio
n = number of terms in the progression.

• The general term of a geometric progression is given by T_n = a^n–1
• The sum to n terms of a geometric progression is given by
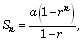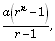  when r < 1 when r > 1
• If three numbers are in geometric progression, the middle number is called the geometric mean of the other two terms.
• If a, b, c are in geometric progression, then where 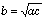is the geometric mean.
• Similarly, if n terms a1, a2, a3, a4,…an are in geometric progression, then the geometric mean of 1 these n terms is given by GM =
• For a decreasing geometric progression the sum to infinite number of terms is
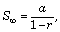  where a = first term and | r | < 1.
• If every term of a GP is multiplied by a fixed real number, then the resulting series is also a GP.
• If every term of a GP is raised to the same power, then the resulting series is also a GP.
• The reciprocals of the terms of a GP is also a GP.
• If three numbers are in GP, then they can be taken as 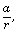a, ar.
• If four numbers are in GP, then they can be taken as
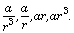
• If five numbers are in GP, then they can be taken as

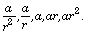
Harmonic Progression (HP)

If the reciprocals of the terms of a series form an arithmetic progression, then the series is called a harmonic progression.
(i) The sequence is a harmonic progression as is in arithmetic progression.

• If a, b, c are in harmonic progression, then b = 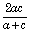where b is the harmonic mean.

Sum of Natural Series

• The sum of the first n natural numbers =
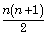
• The sum of the square of the first n natural numbers =
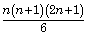
• The sum of the cubes of the first n natural numbers =
• The sum of first n even numbers = n(n + 1)
• The sum of first n odd numbers = n²

Example 1: Find the nth term and the fifteenth term of the arithmetic progression 3, 9, 15, 21…
Solution. In the given AP we have a = 3, d = (9 – 3) = 6
T_n = a + (n – 1)d = 3 + (n – 1)6 = 6n – 3
T₁₅ = (6 × 15 – 3) = 87

Example 2: Find the 10th term of the AP 13, 8, 3, –2,…
Solution. In the given AP, we have a = 13, d = (8 –13) = –5
T_n = a + (n – 1)d = 13 + (n – 1)(–5) = 18 – 5n
T₁₀ = 18 – 5 (10) = –32

Example 3: The first term of an AP is -1 and the common difference is -3, the 12th term is
Solution. T₁ = a = –1, d = –3
T_n = a + (n – 1)d = –1 + (n – 1)(–3) = 2 – 3n
T₁₂ = 2 – 3 × 12 = –34

Example 4: Which term of the AP 10, 8, 6, 4… is –28?
Solution. We have, a = 10,d = (8 – 10) = –2, T_n = –28
T_n = a + (n – 1)d – 28 = 10 + (n – 1)(–2) = n = 20

Example 5: The 8th term of an AP is 17 and the 19th term is 39. Find the 20th term.
Solution. T₈ = a + 7d =17 ...(i)
T₁₉ = a + 18d = 39 ... (ii)
On subtracting Eq. (i) from Eq. (ii), we get 11d = 22 => d = 2
Putting d = 2 in Eq. (i), we get a + 7(2) = 17 = a = (17 – 14) = 3
\First term = 3, Common difference = 2
T₂₀ = a + 19d = 3 + 19(2) = 41

Example 6 Find the sum of the first 20 terms of the AP, 2,–1, –4,–7,
Solution. Here, a = 5, d = (–1–2) = –3 and n = 20
Sn =

Example 7: Find the sum of the series 5, 10, 15, 20,…125.
Solution. Here, a = 5, T_n = 125, d = (10 – 5) = 5
T_n = a + (n – 1)d × 125 = 5 + (n – 1) 5 => n = 25
Sn =

Example 8: Find three numbers in AP whose sum is 36 and product is 1620.
Solution. Let the numbers be (a – d), a, (a + d). Then, (a – d) + a + (a + d) = 36 => 3a = 36 => a = 12
(a – d) × a × (a + d) = 1620 (12 – d) × l2 × (12 + d) = 1620
(144 – d²) – 135 => d2 – 9 + d = ±3
\ Numbers are 9, 12, 15 or 15, 12, 9.

Example 9: Find the nth term and 8th term of the GP –3, 6, –12, 24,–48, …
Solution. In the given GP, we have a = –3, r =
\ T_n = ar^n–1 = (–3)(–2)^n–1
T₈ = (–3)(–2)^8–1 = (–3)(–2)⁷= 384

Example 10: The n^th term of GP is 3/2ⁿ. Find the ratio of 5th to 10th term.
Solution. In the given GP, we have

Example 11: Determine the 9th term of GP whose 8th term is 192 and common ratio 2.
Solution. In the given GP, we have r = 2, T₈ = ar⁷ = 192
=> a(2)⁷ = 192 => a = \ T₉ = ar⁸ =

Example 12: The first term of a GP is 50 and the 4th term is 1350. Determine the 6th term.
Solution. Let a be first term and r be the common ratio.
Then, a = 50 ...(i)
T₄ = ar³ = 1350 ...(ii)
On dividing Eq. (ii) by Eq. (i), we get r³ = 27 => r = 3

Example 13: Find the sum to infinity for the GP
Solution. In the given GP, we have a =

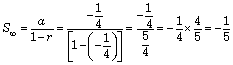
Example 14: In a certain colony of cancevous cells, each cell divides into two every minute. How many cells will be produced from a single cell, if the rate of division continues for 12 min?
Solution. Total number of cells = 2 + (2² + 2³ +2⁴ +...+2¹²)
= 21 + 22 + 23 +....+ 212 =

© UPSCPORTAL.COM