Fundamental Principles of Counting

Fundamental Principle of Multiplication: If there are two jobs such that one of them can be completed in n ways and second job can be completed in n ways, then the two jobs in succession can be completed in m × n ways. Fundamental Principle of Addition: If there are two jobs such that they can be performed independently in m and n ways respectively, then either of the two jobs its can be performed in (m + n) ways.

Example 1: Find the number of ways in which n different prizes can be distributed among m (< n) persons, if each is entitled to receive at most n – 1 prizes. Solution. Total number of ways = m × m × ... to n times = mⁿ The number of ways in which one gets all the prizes = m The required number of ways = mⁿ – m

Example 2: There are 4 candidates for the post of a lecturer in Mathematics and one is to be selected by votes of 5 men. Find the number of ways in which the votes can be given.
Solution. Each man can vote for one of the 4 candidates and this can be done in 4 ways. Similar is the case with every other man. Hence, 5 men can vote in 4⁵ ie, 1024 ways.

Permutations

Each of the arrangements which can bemade by taking some or all number of things is called a permutation. Thus, the permutations which can be made by taking the letters a, b, c two at a time are 6. ie, ab, bc, ac, ba, cb and ca. Each of these presenting a different arrangement of two letters. These six arrangements are called permutations of three things taken two at a time.

Linear Permutation

If the things are arranged in a row/line, then a permutation is called linear permutation. It is simply written as a permutation.

• The number of permutations of n dissimilar things taken r at a time is ⁿP_r.
  ⁿP_r. = n(n – 1)(n – 2)…(n – r – 1) = n!/ ( n-r)!
• Where n! is the product of the first n natural numbers and called ‘n – factorial’ or ‘factorial n’ denoted by n! or n eg, 5! = 5 × 4 × 3 × 2 × 1 = 120 Here, we also define that 10 or 0 is 1. Also, n! is defined only for positive integers. eg, The number of permutations of 6 dissimilar things taken 4 at a time is
  ⁶P₄ = = 6 × 5 × 4 × 3 = 360
• The number of permutations of n dissimilar things taken all at a time is nP_n .
  ⁿP_n = n!/( n-n)!= n!
• eg, The number of permutations of 3 dissimilar things taken all at a time is ³P₃ = 3!/ (3-3)! = 3! = 3 × 2 × 1 = 6
• The number of permutations of n dissimilar things taken r at a time, when repetition of things is allowed any number of times is nr . eg, The number of different telephone numbers formed by taking 3 digits from 1, 2, 3, 4 is 4³ = 64
• If n dissimilar things are grouped into k groups such that al things in the first group are alike,… a₂ in the second group are alike ak in the kth group are alike, then the number of permutation of n such things taken all at a time is
  
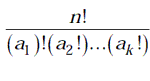
  eg, The number of permutations that can be made using all the letters of the word ‘MANORAMA’ is 8/2.3 (Since, the given word contains 8 letters of which there are 2M’s, 3A’s and three different letters.)

Circular Permutation

If the things are arranged around a circle, then a permutation is called a circular permutation. In circular permutation, there is no first or last place of an object.Hence, the principles of linear permutations are not applicable in circular permutations. In such type of permutations, the relative positions of the things alone need to be taken into consideration and not the actual position.

• The number of circular permutation of n different things taken all at a time around a circle is (n - 1)! . eg, The number of ways in which 6 students sit around the table is (6-1)! ie, 5!. Circular Permutat ion Around a Thread
• If any arrangement of n different things around a circle in the clockwise direction is considered to be not different from the similar arrangement in the anti- lockwise direction, then, in this case, the number of circular permutations of n different things is 1/2(n-1)!.
• In the arrangement of flowers in a closed garland or beads in a necklace, no distinction need to be made between clockwise and anti-clockwise directions. eg, The number of ways in which 8 differently coloured beads be strung on a necklace is
  

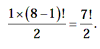
Combinations

Each of the groups or selections that can be made by taking some or all of a number of things is called a combination. Thus, the selections that can bemade by taking the letters a, b, c two at a time are three. ie, ab, bc and ac. These three groups or selections are called the combinations of three things taken two at a time.

• The number of combinations of n dissimilar things taken r at a time is ⁿC_r.

The number of selections of 6 dissimilar things taken 4 at a time is The number of combinations of n dissimilar things taken all at a time is ⁿC_n

The number of selections of 3 dissimilar things taken all at a time is ³C₃=3!/(3-3)!= 1

Distribution of Things into Groups

• The number of ways in which things can be divided into two different groups ofmand n things respectively
  

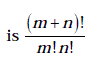
The number of ways of dividing 10 books into two groups each containing 7 and 3 books is

If m = n, then, we have to divide the given items into 2 equal groups, then 2 cases arise

• When the two groups have distinct identity As m= n, we get the number of ways of dividing 2mthings into
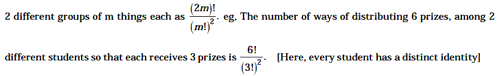
• When the two groups do not have distinct identity. In this case, we have to divide the above result by 2! as the two groups can be interchanged in between themselves in 2! ways. Again as m = n,
  

[Here, no distinction is made between one parcel and other so the order is immaterial. The number of ways in which (m + n + r) things can be divided into three groups containing m, n and r

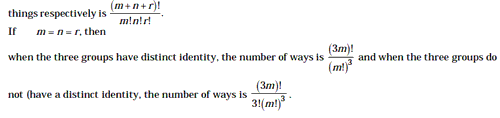
Total Number of Combinat ions

• The total number of combinations of (p + q) things taken any number at a time when p things are alike of one kind and q things are alike of a second kind is (p + 1) q + 1) – 1. eg, There are 4 oranges, 5 pineapples and 7 watermelons in a fruit basket. The number of ways in which a person can choose one or more of the fruits is [(4 + 1) × (5 + 1) × (7 + 1)] – 1 = (5 × 6 × 8) –1 = 239
• The total number of ways of selecting one or more objects from n given objects is (2n – 1). eg, The number of ways in which a man can invite one or more of his 5 friends to dinner is (2⁵ – 1) = 32 – 1= 31 ways.

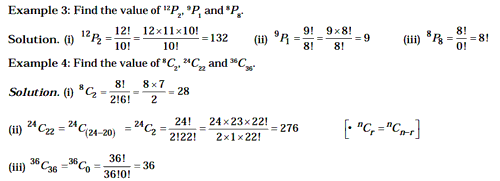
Example 5 An automobile dealer provides cars in 3models and 7 different colours each. Find the number of choices open to a customer.
Solution. Using the fundamental principle, number of choices open to a customer = 7 × 3 = 21

Example 6: How many, permutations can be made
(i) Using all the letters of the word ‘COMPUTER’
(ii) How many begin with C ?
Solution. (i) Since, all the letters are distinct that are 8 in number. The required number of permutations is ⁸P₈ – 8!.
(ii) When C occupies the first place the remaining 7 letters can be arranged among themselves in ⁷P₇ = 7! ways.

Example 7: How many 4 letter permutations can be made from the letters of the word FLOWER?
Solution. Since, all the 6 letters in the word are distinct, the number of permutations

Example 8: Find the number of 3 digit numbers that can be formed from the digits (i) {1, 2, 3, 4, 5} (ii) {1, 2, 3, 4, 5, 6, 7, 8} when the digits are not repeated.

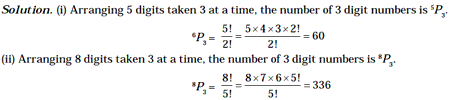
Example 9: Find the number of 3 digit numbers that can be formed from the digits (i) {1, 2, 3, 4, 5} (ii) {1, 2, 3, 4, 5, 6, 7, 8} using the digits any number of times. Solution. (i) The numbers of 3 digit numbers formed by using the given 5 numbers any number of times is 5 × 5 × 5 = 5^3.
(ii) The number of 3 digit numbers formed by using the given 8 numbers any number of times is 8 × 8 × 8 = 83.

Example 10: Find the number of permutations that can be made using all the letters of the word
(i) MISSISSIPI (ii) CHEESE.

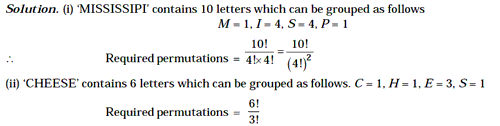
Example 11: How many words can be formed using all the letters of the word ‘MONDAY’ so that
(i) the vowels always come together
(ii) the vowels are never together?
Solution. (i) Given word contains 6 different letters when the vowels OA are always together, we may suppose them to form an entity, treated as one letter. Then, the letters to be arranged are MNDY (OA). These 5 letters can be arranged in
⁵P₅ = 5! = (5 × 4 × 3 × 2 × 1) ways = 120 ways.
The vowels in the group (OA) may be arranged in
²P₂ = 2! = 2 × 1= 2 ways.
Required number of words = 120 × 2 = 240
(ii) The total number of words formed by using all the 6 letters of the given word = 6P6 = 6! = (6 × 5 × 4 × 3 × 2 ×1) = 720
From (i) the numbers of words in which the vowels are always together = 240
:. The number of words in which the vowels are never together = (720-240) = 480

Example 12: In how many ways 10 persons can sit around around table?
Solution. The number of ways in which 10 persons can sit around around table is (10 – 1)! = 9!.

Example 13: Find the number of ways in which 7 women can sit around a round table so that all shall not have the same neighbours in any two arrangements.
Solution. Circular arrangement of 7 women in one direction only (7-1)!/2 = 6!/2 = 720/ 2 = 360

Example 14: Find the number of ways in which 5 players out of 8 players can be selected to form a team is
Solution. The required number of ways is

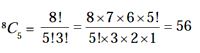
Example 15: Find the number of ways in which a committee consisting of 3men and 2 women can be formed from 5 men and 4 women.
Solution. 3 men out of 5 can be selected in ⁵C₃ ways. 2 women out of 4 can be selected in ⁴C₂ ways. By the fundamental principle, these two can be done in ¹C₃ × ⁴C₂ ways.

Example 16: Find the number of ways in which 6 players out of 10 players can be selected so as 2 particular players are always included.
Solution. Since, 2 particular players are always included the choice reduces to only 4 players among 8 players which can be done in ⁸C₄ ways.

Example 17: A set of m parallel lines intersect another set of n parallel lines in a plane. Find the number of parallelograms formed.
Solution. For a parallelogram to be formed we should have two parallel lines to intersect another two parallel lines. Two out of m parallel lines and two out of another n parallel lines can be chosen in nC2 × nC2 ways. The number of parallelograms formed is ^mC₂ × ⁿC₂ .

Example 18: The number of ways in which the sixfaces of a cube be painted with six different colours.
Solution. Number of ways = 6! / 6! = 1 (All faces are alike).

Example 19: There are stalls for 10 animals in a ship. The number of ways the shipload can bemade if there are cows, calves and horses to be transported, animals of each kind being not less than 10.
Solution. Each stall can be filed in 3 ways as there are three types of animals (animals of each category being not less than 10). Shipload, ie, filling up of 10 stalls,can be made in 3 × 3 × ... up to 10 times = 3¹⁰.

Example 20: An examination paper contains 8 question of which 4 has 3 possible answers, 3 have 2 possible answers each and the remaining one question has 5 possible answer. The total number of possible answers to all the questions
Solution. Total number of possible answers = 3⁴ × 2³ × 5¹ = 81 × 8 × 5 = 3240

Example 21: Manoj, Manika, Shivangi, Rohit are to give speeches in a class. The teacher can arrange the order of their presentation in number of ways.
Solution. Required number of ways = 4! = 24

Example 22: If there are 12 persons in a party, and if each of them shakes hands with each other, then number of handshakes happen in the party.
Solution. Total number of handshakes = The number of ways of selecting 2 persons from among 12 persons = ¹²C₂ = (12×11)/(2×1) = 66

© UPSCPORTAL.COM