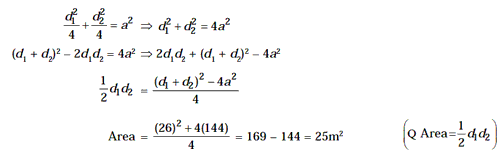(Online Course) CSAT Paper - II : Basic Numeracy: Area of Plane Figures

Area

The area of a plane figure is the measure of the surface enclosed by its boundary. The area of a triangle or a polygon is the measure of the surface enclosed by its sides.

1. Triangle

 

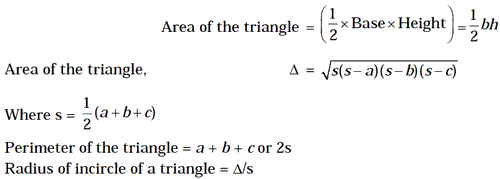
2. Right-Angles Triangle
 

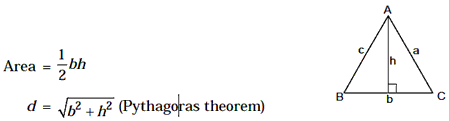
Hypotenuse,
Perimeter = b + d + h

3. Isosceles Right-Angled Triangle

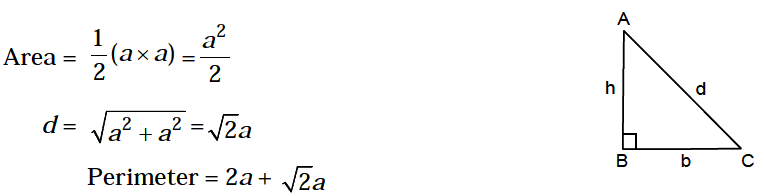
4. Equilateral Triangle

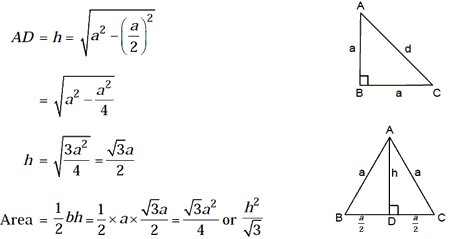
Perimeter = 3a
Radius of incircle of an equilateral triangle of side a = a/2 Ö3
Radius of circumcircle of an equilateral triangle of side a = a/Ö3

5. Square

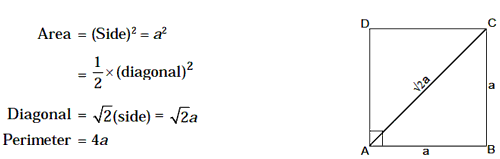
6. Rectangle

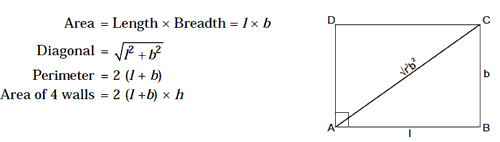
7. Parallelogram

 

 

 

 

 

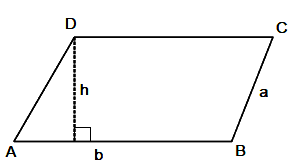
Opposite sides are parallel and equal and opposite angles are equal.

Area = Base × Height = b × h
Perimeter = 2 (a + b)
 

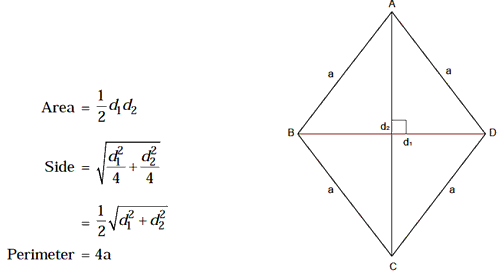
8. Rhombus

All sides are equal and opposite angles are equal. Diagonals bisect each other at right angles.

9. Trapezium
 

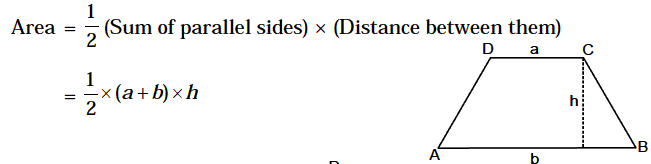
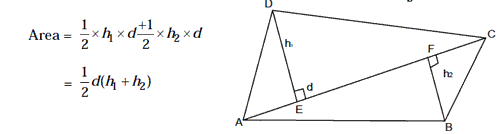
10. Qudrilateral

11. Circle
 

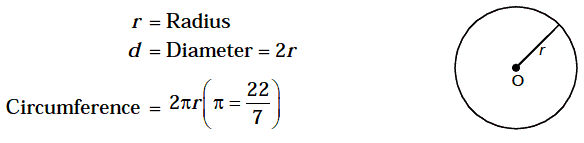
12. Semi-Circle

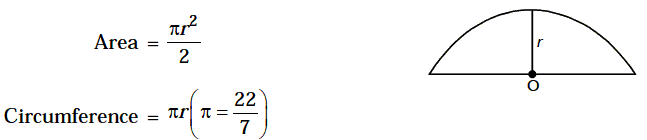
13. Sector

r = Radius, l = Length of the arc
q = Central angle
Area of the sector =1/2 (Arc length* r )= Πr² q/360
where are length= 2Πrq/360

 

 

 

 

 

 

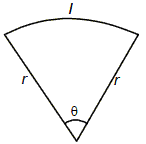
Example 1: One side of a rectangular field is 16 m and one of its diagonal is 20 m. Find the area of the field. Solution. BC² = AC² – AB² = (20)² – (16)² = 400 – 256 = 144

Example 2: The length and breadth of a room are in the ratio of 3 : 2. Its area is 864 m2. Find its perimeter.
Solution. Let the length be 3x m and breadth be 2x m.

Area = (3x × 2x) = 6x² = 864= x² = 144 = x = 12
Length = 3x = (3 × 12) m = 36 m
Breadth = 2x = (2 × 12) m = 24 m
Perimeter = 2 (l + b) = 2 (36 + 24) = 120 m

Example 3: Find the circumference of a circle whose diameter is 14 m.
Solution. r =diameter/2=14/2 = 7m
Area = Πr2=22 /7 *7 *7 =154m2
Circumference = 2Πr == 44m

Example 4: The areas of two concentric circles are 154m2 and 308m2 respecively. Find the width of the ring made by them.
Solution. The radius of inner circle r = Ö154/Π = 7m
Another circle is outside this circle.
If the width of the ring be w then area of the ring

Πw (2r + w) = 308 – 154
22/7*w (14 +w)= 154
w = 289 m

Example 5: Find the area of a regular hexagon inscribed in a circle whose radius is 15 cm.
Solution: OC = r = 15 cm
Since, regular hexagon is inscribed in the circle. D BOC is an equilateral triangle
So, BC = a = 15 cm

 

 Example 6: A rectangular grassy plot 120m × 80m has a gravel path 3m wide all round it on the inside.
Find the cost of gravelling the path at Rs. 2 per m².
Solution. Area of the plot= (120 × 80)m² = 9600 m²
Area of the plot (excluding path)= [(120 – 6) × (80 – 6)] m² =(114 × 74) m² = 8436 m²
Area of the path= (9600 – 8436) m² = 1164 m²
Cost of gravelling the path= Rs. (1164 × 2) = Rs. 2328

Example 7: Find the length of the diagonal of a square whose area is 441 m²
Solution. Solution. Area of the square (side)2= 441m2
Side = 441 = 21 m
Diagonal of a square= Ö2*side = 21Ö 2m

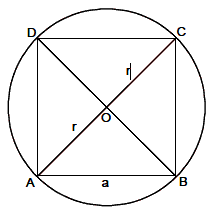
Example 8: Find the area of a square that can be inscribed in a circle of radius r.
Solution. Let ABCD be a square inscribed in a circle of radius r.

 

 

 

 

 

 

Diagonal AC =  2(OC) = 2r
Let AB = a, then AC =Ö2a
Ö2a = 2r , a = 2/Ö2r = Ö2r
Hence, Area = a² = ( 2r)²= 2r²

Example 9: Find the area of a triangle whose sides are 6m, 11m and 15m in length.
Solution:

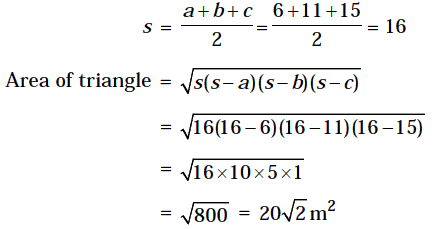
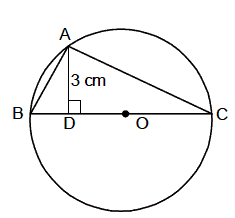
Example 10: Find the area of a right angled triangle which is inscribed in a circle of radius 4 cmand altitude drawn to the hypotenuse is 3 cm.
Solution.

 

 

 

 

 

 

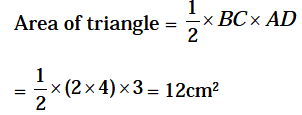
Example 11: Find the percentage increase in the area of a triangle, if its each side is doubled.
Solution: Let a, b, c be the sides of the given triangle

Example 12: The perimeter of a rhombus is 48 m and the sum of the lengths of its diagonals is 26 m. Find the area of rhombus.
Solution. The perimeter of rhombus = 4a = 48
Þ a = 12m
If the diagonals of rhombus are d₁ and d₂, then d₁ + d₂ = 26m (given)
Now, by the relation between diagonals and sides of rhombus