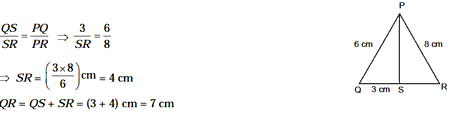(Online Course) CSAT Paper - II : Basic Numeracy: Concepts of Geometry

Point

A point is defined by its position. It has no length, width or thickness. A straight line joining two points is the shortest distance between them. Three ormore points are said to be collinear, if there is a line which contains all of them.

Line

A line is defined by its length and has no breadth. It has length units. (metre, foot, centimetre kilometre, etc.). A line contains infinite points. Through a given point, there pass infinite lines. One and only one straight line passes through two distinct points. Three ormore lines are said to be concurrent, if they pass, through one point and that point is called the point of concurrence. Two lines are said to be intersecting lines, if they have a common point.

Angle

When two straight lines meet at a point, they are said to form an angle. Angles generally are measured in degrees. There are 180° in a straight line and a full circle constitutes 360°.

1. Two angles are said to be complementary, if their sum is 90°. Complement of x is (90° – x).

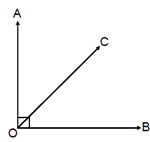
In the adjoining figure, ÐAOC + ÐBOC = 90°.
Ð AOC and Ð BOC are complementary to each other

2. Two angles are said to be supplementary, if their sum is 180°. Supplement of x is (180° – x).

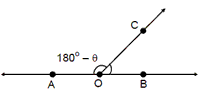
ÐAOC +Ð BOC = 180°.
ÐAOC and ÐBOC are supplementary to each other.

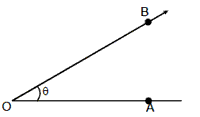
3. An angle which less than 900, is called acute angle
Ð AOB < 90° Ð AOB is an acute angle.

4. An angle which is greater than 90° is called obtuse angle.
ÐAOB > 90° ÐAOB is an obtuse angle.

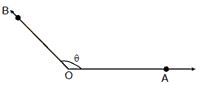
5. An angle which is exactly 90° is called Right Angle and the two lines are said to be Perpendicular to each other.
Ð AOB = 90° Ð AOB is a right angle and OA and OB are perpendicular to each other.

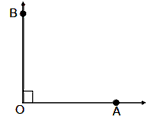
6. An angle which is greater than two right angles but less than four right angles is said to be Reflex Angle.
180° < Ð AOB < 360° Ð AOB is reflex angle.


7. Angles which lie on either side of a common line are called Adjacent Angles. Ð AOC and Ð COB have a common vertex ‘O’ and a common arm OC uuur . Hence, they are adjacent angles.

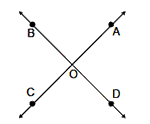
8. If two lines intersect, then Vertically Opposite Angles are equal in magnitude. Ð AOB = Ð COD and Ð BOC =Ð AOD are two pairs of vertical opposite angles.

Angles Bisector

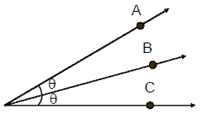
A line which cuts an angle into two equal angles is called an angle bisector. An angle bisector can be internal
or external. Ð AOC = Ð COB = OC uuur is the internal angle bisector.

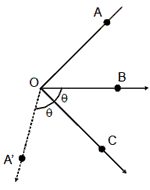
Ð A’ OC = Ð COB = OC uuur is the external angle bisector.

Parallel Lines

Two lines in the same plane are said to be parallel, if they never meet, however any far they are extended in either direction. They remain at same distance for the whole length. The sign of parallel is ‘||’. A line which cuts a pair of parallel lines is called a transversal. If AB || CD and EF a transversal. Then,

1. Four pairs of corresponding angles are formed which are equal. The corresponding angles are Ð1= Ð 5, Ð 2 = Ð 6, Ð 4 = Ð8 and Ð 3 = ÐS 7.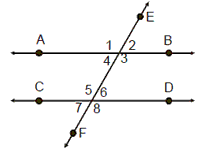

2. Four pairs of alternate angles are formed which are equal. The alternate angles are
Ð 1 = Ð 7, Ð 2 = Ð 8, Ð 3 = Ð 5 and Ð4 = Ð 6
3. The sum of the interior angles on the same side of the transversal equal to two right angles.
Ð 3 + Ð 6 = 180° and Ð 4 + Ð 5 = 180°.
4. The sum of the exterior angles on the same side of the transversal equal to two right angles.
Ð 1 + Ð 8 = 180° and Ð 2 + Ð 7 = 180°.

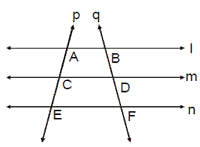
Also, straight lines which are parallel to the same straight line are parallel to one another and intercepts made by two transversals on three or more parallel lines are proportional. In the adjoining figure, l, m and n are three parallel lines and p and q are two transversals than AC/CE=BD/DF

Polygons

A polygon is a closed plane figure bounded by straight lines.
Convex Polygon: A polygon in which none of its interior angles is more than 1800.
Concave Polygon A polygon in which atleast one angle is more than 180°.
Regular Polygon A regular polygon has all its sides and angles equal.

• Each exterior angle of a regular polygon = 360°/number of sides
• Each interior angle = 180° – (exterior angle).
  In a Convex Polygon of n sides, we have
  (a) Sum of all interior angles = (2n – 4) × 90°
  (b) Sum of all exterior angles = 360°
  (c) Number of diagonals of a polygon on n sides = n(n-3)/2

A polygon is called a Triangle, Quadrilateral, Pentagon, Hexagon, Heptagon, Octagon, Nonagon and Decagon according as it contains 3, 4, 5, 6, 7, 8, 9, 10 sides respectively.

Triangles

A triangle is a plane figure bounded by three straight lines.

1. In a triangle, the side which is opposite to the largest angle is the longest side and the side which is opposite to the smallest angle is the shortest side.
2. The sum of the lengths of two sides of a triangle is always greater than the length of the third side.
3. The sum of the internal angles in a triangle is 180° and that of the external angles is 360°.
4. The difference of any two sides of a triangle is always lesser than the third side.
5. If one side of a triangle is produced, the exterior angle formed is equal to the sum of the interior opposite angles.

Scalene Triangle: When all the sides (and angles) of a triangle are unequal. Isosceles Triangle: When two sides of a triangle are equal and two angles opposite to the two equal sides are equal. Equilateral Triangle: When all the sides (and angles) of a triangle are equal.
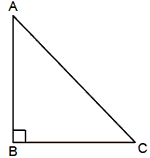
Each interior angle is 60°. Right-Angled Triangle When one angle of a triangle is right angle. In the figure Ð B = 90° and Ð A + Ð C = 90°. By Pythagoras Theorem: AB2 + BC2 = AC2 where AC is the hypotenuse.

A triplet is a set of numbers which will satisfy the Pythagoras Theorem. The frequently used triplets are (3, 4, 5), (5, 12, 13), (7, 24, 25), (8, 15, 17), (9, 40, 41), (11, 60, 61), (12, 35, 37), (16, 63, 65), (20, 21, 29). The multiples of triplets are also triplets eg, (6, 8, 10) is a multiple of (3, 4, 5) and a triplet.

Congruency of Triangles Two triangles are congruent, if

• Three sides of one triangle are respectively equal to three sides of the other (SSS).
• Two sides and the included angle of the one triangle is equal to the corresponding two sides and the included angle of the other (SAS).
• Two angles and a side of one triangle is equal to the corresponding two angles and a side of the other (ASA).
  Similarity of Triangles: Two triangles are said to be similar, if their corresponding angles are equal and their corresponding sides are proportional, ie, they have the same shape but may have different sizes.

1. Ratio of the areas of two similar triangles is equal to the ratio of the squares of any two corresponding sides.
2. Ratio of areas of two similar triangles is equal to the ratio of the squares of the corresponding altitudes and medians.
3. The internal bisector of an angle of a triangle divides the opposite side internally in the ratio of sides containing the angle.
4. The lines joining the mid points of any two sides of a triangle is parallel to the third side and equal to half of it.

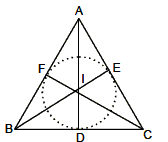
Altitude: It is the perpendicular dropped to a side of a triangle from the vertex opposite to that side. All the three altitudes of a triangle meet at a point called the orthocenter of the triangle.

In DABC, AD, BE and CF are altitudes and meet at orthocentre O. Angle Bisector: It is the bisector of an angle contained in the vertex of a triangle. All the three angle bisectors of a trianglemeet at a point called the incentre of the triangle. The incentre is the centre of a circle which can be perfectly inscribed in the triangle. in centre I.

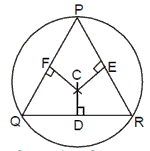
Perpendicular Bisector: It is the line passing through themid point of the side of a triangle and perpendicular to it.All the three perpendicular bisectors of a triangle meet at a point called the circumcentre of the triangle. The circumcentre is the centre of a circle which can be perfectly circumscribed about the triangle. The circumradius = PC = QC= RC and Ð QCR = 2 Ð P. In D PQR the angle bisectors meet at circumcentre C. Also, D, E and F are mid points of QR, RP and PQ respectively.

Median: It is the line joining themed point of a side of a triangle with the vertex opposite to that side. All the three medians of a triangle meet at a point called the centroid of the triangle. They also intersect each other such that each median is split in a ratio of 1 : 2 from the base side. In D ABC, AD, BE and CF are themedians and meet at the centroid G. Also,

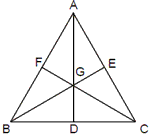
By Apollonius theorem,
AB² + AC² = 2AD² + 2 [BD² ]

Quadrilaterals

It is a plane figure bounded by four straight lines. It has four sides and four internal angles. The sum of the internal angles of a quadrilateral is 360°. Parallelogram: A quadrilateral in which the opposite sides are equal and parallel is called a parallelogram. In a parallelogram
(i) The opposite sides are parallel and of equal length. AB = DC and AD = BC.

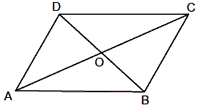
(ii) The sum of any two adjacent interior angles is equal to 180°.
Ð A + Ð B = Ð B + Ð C = Ð C + Ð D = Ð D + Ð A
(iii) The opposite angles are equal in magnitude Ð A = Ð C and Ð B = Ð D.
(iv) The diagonals of a parallelogram are not equal in magnitude, but they bisect each other. AC ¹ BD but AO = OC and OB = OD.
Rhombus: A parallelogram in which all the sides are equal is called a rhombus.

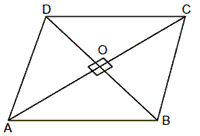
(i) The opposite sides are parallel and all the sides are of equal length. AB = BC= CD= DA
(ii) The sum of any two adjacent interior angles is equal to 180°.ÐA + Ð B = Ð B + Ð C = Ð C + Ð D = Ð D + Ð A.
(iii) The opposite angles are equal in magnitude. Ð A = Ð C and Ð B = Ð D.
(iv) The diagonals bisect each other at right angles and form four right angled triangles. They are not of equal magnitude.
(v) Area of the four right triangles ÐAOB = ÐBOC = Ð COD =Ð DOD and each equals 1/4^th the area of the rhombus.
(vi) Sum of the squares of sides is equal to the sum of the squares of its diagonals.
Rectangle: A parallelogram in which the adjacent sides are perpendicular to each other.

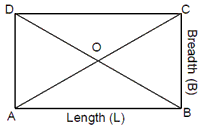
(i) The opposite sides are parallel and of equal length. AB = CD and AD = BC.
(ii) The adjacent sides are perpendicular ieÐ A = Ð B = Ð C = Ð D = 90°.
(iii) The diagonals of a rectangle are of equal magnitude and bisect each other. AC = BD and AO = OC = BO = OD.
Square: A parallelogram in which all the sides are equal and perpendicular to each other.

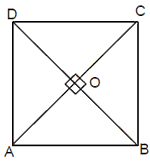
(i) The opposite sides are parallel and all the sides are of equal length. AB = BC = CD = DA.
(ii) The diagonals bisect each other at right angles and form four isosceles right angled triangle.
(iii) The adjacent sides are perpendicular ie, Ð A = ÐB = Ð C = Ð D = 90°.
(iv) The diagonals of a square are of equal magnitude. AC = BD.

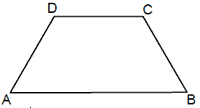
Trapezium: It is a quadrilateral where only one pair of opposite sides are parallel. ABCD is a trapezium as AB || DC.

Circles

A circle is a set of points which are equidistant from a given point. The given point is known as the centre of that circle. The angle in a circle is 360°.

Arcs, Chords and Central Angles

• In equal circles (or in the same circle), if two arcs are equal, the chords associated with the arcs are equal and vice-versa.
• In equal circles (or in the same circle), if two arcs subtend equal angles at the centre, then they are equal.

Angles in a Circle

• The angle which an arc of a circle subtends at the centre is double that which it subtends at any point on the remaining part of the circle.
• Angles in the same segment of a circle are equal.
• The angle in a semicircle is a right angle.

Chords in a Circle

• A straight line drawn fromthe centre of a circle to bisect a chord which is not a diameter is at right angle to the chord. Conversely, the perpendicular to a chord from the centre bisects the chord.
• Equal chords of a circle are equidistant from the centre. Conversely, the chords that are equidistant from the centre are equal.
• If two chords of a circle AB and CD intersect internally or externally the circle when produced at a point E, then AE × EB= DE× EC.

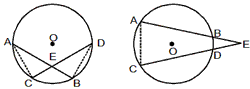
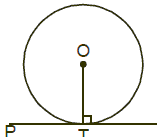
Tangents to a Circle

(i) The tangent at any point of a circle is perpendicular to the radius through the point of contact OT^PT.

(ii) If two tangents are drawn to a circle from an outside point, the length of the tangents from the external point to their respective points of contact are equal. ie, PA= PB.

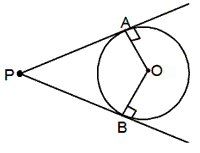
(iii) The angle which a chordmakes with a tangent at its point of contact is equal to any angle in the alternate segment.

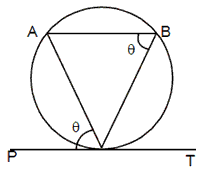
ÐPTA = Ð ABT where AT is the chord and PT the tangent to the circle.

(iv) If PT is a tangent (with P being an external point and T being the point of contact) and PAB is a secant to circle(with A and B as the points where the secant cuts the circle), then PT2 = PA × PB.

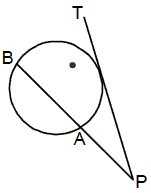
Pairs of Circles

(i) If two circles touch each other, the point of contact of the two circles lies on the straight line through the centres of the circles, ie,. the points A, C, B are collinear.

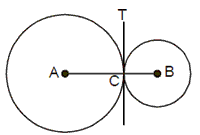
(ii) In a given pair of circles there are two types of tangents. The direct tangents and the cross (or transverse) tangents. In the figure the direct tangents are AB and CD and EH and GF are the transverse tangents.

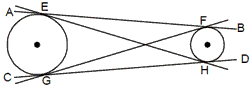
(iii) When two circles of radii r₁ and r₂have there centres at a distance d, the length of the direct common tangent = Öd² - r² where r = r₁– r₂ and the length of transverse tangent ==Öd² - (r₁+r₂) . If the two circles touch, then d = r₁+ r₂ Cyclic Quadrilateral: A quadrilateral whose vertices be on the circumference of a circle is called a cyclic quadrilateral. The opposite angles of a cyclic quadrilateral are supplementary. a+ b = 1800.

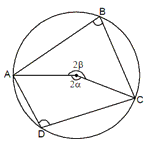
Example 1: An angle q° is one-fourth of its supplementary angle. What is the measure of angle q°?
Solution. If the sum of two angles is 180°, the angles are said to be supplementary.
The supplementary angle of q° is (180°– q').

Example 2: In the given figure AB and CD are parallel lines. If Ð EGB = 50°, then find Ð CHG.

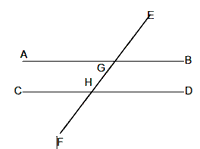
Solution. Ð AGH= Ð EGB (Vertically opposite angles) Ð AGH = 50°. Now, Ð AGH + Ð CHG = 180°
(Interior angles on the same side of the transversal are supplementary).
50° + Ð CHG = 180°
Ð CHG = 180° – 50° = 130°.

Example 3: In the figure given find x.

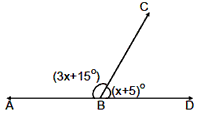
Solution. Ð ABC + Ð DBC = 180°(3x + 15)° + (x + 5)° = 180°
4x = 160° = x = 40°

Example 4: In the following figure A, B, C, D are the co cyclic points. Find the value of x.

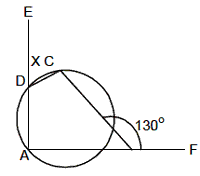
Solution.
Ð ABC +Ð CBF = 180° ÐABC = 180° – 130° = 500
Now, in ÐABCD, Ð ABC +Ð ADC = 180°
Ð ADC = 180° – 50° = 130°
Now, Ð ADC + ÐCDE = 180° x = 180° – 130° = 50°

Example 5: Find the value of x in the given figure,

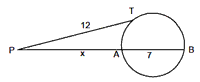
Solution. Since PT is a tangent and PAB is a secant to the circle PT2 = PA . PB 144 = x (x + 7) = x2 + 7x – 144 = 0 (x + 16) (x – 9) = 0
Þ x = 9 (\ x = – 16 is not possible)

Example 6: In the give figure, AD || BC. Find the value of x

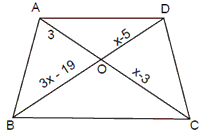
Solution. Here, AD || BC,

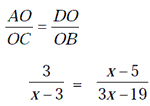
9x – 57 = x² – 8x + 15 = x² – 17x + 72 = 0
Þ (x – 8)(x – 9) = 0
Þ x = 8, 9

Example 7: In the figure given ÐBAC : ÐABC = 2 : 3. Find the measure of ÐABC.

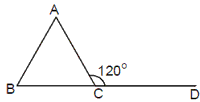
Solution. Let Ð A = 2x and Ð B = 3x
Then, 2x + 3x = 120° [exterior angle is equal to the sum of the interior opposite angles]
Þ5x = 120°
Þ x = 24°
Ð ABC = 3x = 3 × 24° = 72°

Example 8: In D PQR, if PQ = 6 cm, PR = 8 cm, QS = 3 cm and PS is the bisector of Ð QPR, then what is the length of QR?
Solution. Since, PS is the angle bisector of Ð QPR.