(Online Course) CSAT Paper - II : Basic Numeracy: Fractions

A fraction is a part of the whole (object, thing, region). It forms the part of basic aptitude of a person to have and idea of the parts of a population, group or territory. Civil servants must have a feel of ‘fractional’ thinking.

eg, 5/12 , here ‘12’ is the number of equal part into which the whole has been divided, is called denominator and ‘5’ is the number of equal parts which have been taken out, is called numerator.

Example1: Name the numerator of 3/7 and denominator of 5/13.

Solution: Numerator of 3/7 is 3.

                Denominator of 5/13 is 13.

Lowest Term of a Fraction:

Dividing the numerator and denominator by the highest common element (or number) in them, we get the fraction in its lowest form.

eg, To find the fraction 6/14 in lowest form Since ‘2’ is highest common element in numerator 6 and denominator 14 so dividing them by 2, we get 3/7 Which is the lowest form of 6/14.

Equivalent Fractions:

If numerator and denominator of any fraction are multiplied by the same number then all resulting fractions are called equivalent fractions.

eg, 1/2, 2/4, 3/6, 4/8 all are equivalent fractions but 1/2 is the lowest form.

Example 2: Find the equivalent fractions of 2/5 having numerator 6.
Solution: We know that 2 × 3 = 6. This means we need to multiply both the numerator and denominator by 3 to get the equivalent fraction.
Hence, required equivalent fraction = 2/5 = 2 x 3/ 5 x 3 = 6/15

Addition and Subtraction of Fractions

Here two cases arise as denominators of the fraction are same or not.
Case I: When denominators of the two fractions are same then we write denominator once and add (or subtract) the numerators.

eg,  2/7 + 3/7 = 5/7

Case II: If denominators are different, we need to find a common denominator that both denominators will
divide into.

eg,                     1/6 + 3/8

We can write,     1/6 = 2/12, 3/18 = 4/24

                           3/8 = 6/16 = 9/24

                           1/6 + 3/8 = 4/24 + 9/24 = 13/24

Example 3: Calculate 1/2 - 3/7

Solution. 1/2 = 1x 7 / 2 x 7 = 7/14 and 3/7 = 3 x 2 / 7 x 2 = 6/14

Therefore:            1/2 + 3/7 = 7/14 + 6/14 = 1/14

Multiplication and Division of Fractions

To multiply fractions, the numerators are multiplied together and denominators are multiplied together.

eg,                    1/6 x 3/8 = 1 x 3 / 6 x 8 = 3/48 = 1/16

In division of fraction, the numerator of first fraction is multiplied by the denominator of second fraction and gives the numerators. Also denominator of first fraction is multiplied by the nemerator of second fraction and gives the denominator.

                            1/16 ÷ 3/8 becomes 1/6 x 8/3 = 8/18 = 4/9

Proper and Improper Fractions

The fractions in which the number in numerator is less than that of denominator, are called proper fractions. Also if the number in numerator is greater than that of denominator, then the fractions are called improper fractions.

eg, 4/3 is an improper fraction while 3/4 is a proper fraction.

Mixed Numbers

A mixed number is that, which contains both a whole number and a fraction.

eg, 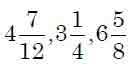          are mixed numbers.

Example 4: Which of the following are proper and improper fractions?
(a) 7/9 (b) 6/5 (c) 12/7 (d) 5/13

Solution. (a) and (d) are proper fractions as numerator is less than denominator.
Also, (b) and (c) are improper fractions as numerator is greater than denominator.

Illusration 5: Are 7/13 and mixed number?

Solution. 7/13 is only a proper fraction as it does not contain any whole number, while is a mixed number as it contains ‘4’ as a whole number and 5/6 is a fraction.

Decimal Fractions

The fractions in which denominators has the power of 10 are called decimal fractions.

eg, 0.25 = nought point two five = 25 /100 = 1/4 = one quarter

        0.1 = nought point one = 1/10 = one-tenth.

For converting a decimal fraction into simple fraction, we write the numerator without point and in the denominator, we write ‘1’ and put the number of zeros as many times as number of digits after the point in the given decimal fraction

eg, 0.037 = 37 /1000, 0.1257 = 1257 /10000

Example 6: Convert the each of the following decimal fractions into simple fractions.
(a) 5.76 (b) 0.023 (c) 257.5
Solution.
(a) 5.76 = 576 /100 = 288 / 50 = 144/ 25 (b) 0.023 = 23 /1000 (c) 257.7 = 2575/ 10 = 515/ 2

Addition or Subtraction of Decimal Fractions

In the addition or subtraction of decimal fractions, we write the decimal fractions in such a way that all the decimal points are in the same straight line then these numbers can be add or subtract in simple manner.

Example 7: Solve 0.68 + 0.062 + 0.20
Solution. 0.680
            +0.062
            +0.200
              0.942

Multiplication of Decimal Fractions

To multiply by multiplies (powers) of 10 the decimal point is moved to the right by the respective number of zero.

Example 8: 0.75 × 10 = ?

Solution. 0.75 × 10 = 7.5 (The decimal point is shifted to right by one place)
To multiply decimals by number other than 10. We ignore the decimal point and multiply them in simple manner and at last put the points after the number of digits (from right) corresponding to the given problem.

Example 9: Multiply 8 and 10.24

Solution. First we multiply 8 and 1024
                                    8 × 1024 = 8192
Now,                           8 × 10.24 = 81.92 (We put decimal points after two digits from right as in given question).

Example 10: 12.4 × 1.62
Solution. We know that
                124 × 162 = 20088
                12.4 × 1.62 = 20.088

Division of Decimal Fractions

Division of decimal numbers is the reverse of the multiplication case ie, we move the decimal point to the left while dividing by multiplies of 10.

Example 11: 25.75 ÷ 10 = ?

Solution. 25.75 ÷ 10 = 2.575

When a decimal number is divided by an integer, then at first divide the number ignoring the decimal point and at last put the decimal after the number of digits (from right) according at in the given problem.

Example 12: Divide 0.0221 by 17
Solution. First we divide 221 by 17 ie, without decimal 221 ÷ 17 = 13
Now, we put decimal according as in the given problem
                                            0.0221 ÷ 17 = 0.0013

If divisor and dividend both are decimal numbers then first we convert them in simple fraction by putting number of zero in the denominator of both. Then divide by the above manner.

Example 13: Divide by 0.0256 by 0.016

Solution. 0.0256 / 0.016 = 256 x 1000 / 16 x 10000 = 256 / 160 = 25.6 / 16 =1.6

Example 14: Divide 70.5 by 0.25

Solution.70.5 / 0.25 =  705 / 100 x 25 / 10 = 7050 / 25 = 282

To Find HCF and LCM of Decimal Fractions

First we make the decimal digits of the given decimal numbers, same by putting some number of zero if necessary. Then find HCF or LCMignoring decimals. And at last put the decimal according as the given numbers.

Example 15: Determine HCF and LCM of 0.27, 1.8 and 0.036.

Solution. Given numbers are 0.27, 1.8 and 0.036.

or,                                        0.270, 1.800 and 0.036.

 These numbers without decimals are 270, 1800 and 36.
Now,                                       HCF of 270, 1800 and 36 = 18
                                                HCF of 0.270, 1.800 and 0.036 = 0.018

Therefore:                                 LCM of 270, 1800 and 36 = 18 × 5 × 2 × 3 × 10 = 5400

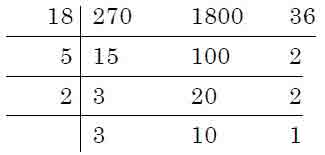
Therefore:                                  LCM of 0.270, 1.800 and 0.36 = 5.400 or 5.4

Terminating and Non-Terminating Recurring Decimals

If decimal expression of any fraction be terminated then fraction is called terminating.
as                                                         5/16 = 0.3125
But if we take example 33 ÷ 26, then

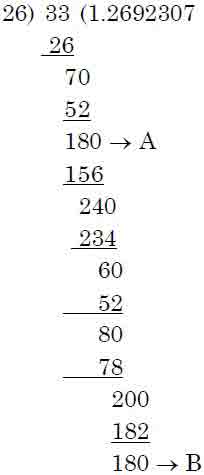
In this division, we see that remainder at the stages A and B are same. In the continued process of division by 26, the digits 6, 9, 2, 3, 0, 7 in the quotient will repeat onwards.

Therefore:    33 / 26 = 1.2692307692307...

This process of division is non terminating. Therefore, such decimal expressions are called non terminating repeating (recurring) decimals. In repeating digit, we put (–) bar.

 ie, 33 / 26 = 1.2692307

Example 16: Write the following fractions in decimal form and till that these are terminating or non terminating recurring.

(a) 2 / 3 (b) 4 / 5 (c)  3 / 11 (d) 17 / 90

Solution. (a) 2 3 = 0.6666.... = 0.6 non terminating recurring

                (b) 4 5 = 0.8 terminating

                (c) 3 / 11 = 0.272727... = 0.27 non terminating recurring

                (d) 17 90 = 0.1888... 0.18 non terminating recurring

Non-Terminating, Non-Recurring Decimals

Every fraction can be put in the form of terminating or non-terminating recurring decimals ie, these decimalnumbers can be put in the form of p/q . These are called rational numbers. But some decimals numbers are there that can’t be put in the form of p/q , these are non-terminating, non-recurring decimals. Also these are called irrational numbers.

eg, 0.101001000100001...

To convert non-terminating recurring decimals into simple fraction

First write the non-terminating recurring decimal in bar notation. Then write the digit ‘a’ in the denominators
as many times as number of digits recurring in the numerator. Also don’t put decimal in the numerator.

Example 17 Convert the following in simple fraction

(i) 0.33333...                         (ii) 0.181818...

Solution.
(i) 0.33333... = 0.3 = 3 / 9 = 1 / 3                   (ii) 0.181818... = 0.18 = 18 / 99 = 2 / 11

Mixed Recurring Decimals

A decimal fraction in which some digits are not repeated and some are repeated, called mixed recurring decimal.

How to Convert Mixed Recurring Decimal into a Simple Fraction?

First we subtract non repeated part from the number (without decimal) and put number 9 as many times as number of recurring digits and also put the number ‘0’ as many times odd number of non recurring digits.

Example 18: Convert the following in simple fraction
(i) 0.18                                                     (ii) 3.0072

Solution. (i) 0.18 = 18 -1 / 90 = 17 /  90

                (ii) 3.0072 = 3 + 0.0072 = 3 + 72 / 9900 = 3 + 2 / 275 =

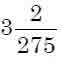
Example 19: Arrange 2 ,13 ,4 3 15 5 and 15 16 in ascending order.

Solution. We know that 2 / 3 = 0.67
                                  13 / 15 = 0.86
                                      4 / 5 = 0.80
                                    15 16 = 0.94

Here, it is clear that 0.67 < 0.80 < 0.86 < 0.94

So,                            2/3 < 4/5 < 13/15 < 15/16

Example 20: Arrange 7 / 9, 8 / 11, 5/13 and 2 / 7 is descending order.

Solution. We know that             7 / 9 = 0.77
                                                 8 /11 = 0.72
                                                5 / 13 = 0.38
                                                  2 / 7 = 0.28

Here it is clear that 0.77 > 0.72 > 0.38 > 0.28

So,                      7/9 > 8/11 > 5/13 > 2/7