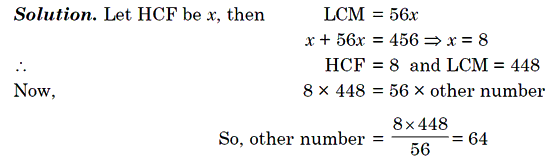(Online Course) CSAT Paper - II : Basic Numeracy: HCF & LCM

Highest Common Factor

The highest common factor of two or more given numbers is the largest of their common factors. It is known as GCD also.

eg,                              Factors of 20 are 1, 2, 4, 5, 10, 20
                                   Factors of 36 are 1, 2, 3, 4, 6, 9, 12, 18, 36
Here greatest and common factor of 20 and 36 is 4.
Therefore,                   HCF of 20 and 36 is 4.

Least Common Multiple

The least common multiple of two or more given numbers is the least of their common multiples.

eg,                         Multiple of 25 are 25, 50, 75, 100, 125, 150, 175, ....
                             Multiple of 30 are 30, 60, 90, 120, 150, 180, 210, ....
Here 150 is least common multiple of 25 and 30
Therefore,             LCM of 25 and 30 is 150.

Using Division Method

Example 1: Determine the HCF and LCM of 36, 48, 64 and 72.

Solution. To find HCF

• The least number which is exactly divisible by a, b and c is the LCM of a, b, c.

• The greatest number that will divide a, b, c is the HCF of a, b, c.

• If x is a factor of a and b, then x is also a factor of a + b, a – b and ab.

• HCF of given numbers must be a factor of their LCM.

• The product of the LCM and HCF of two numbers is equal to the product of the two numbers.

Example 3: LCM of two numbers is 56 times of their HCF. Sum of LCM and HCF is 456. If one of them is 56. Find the other.