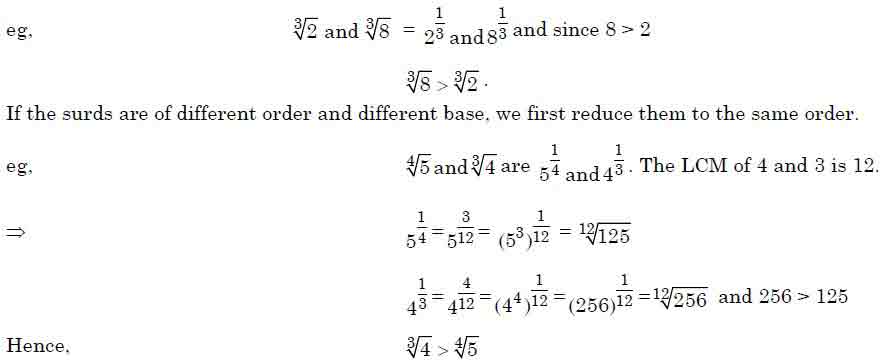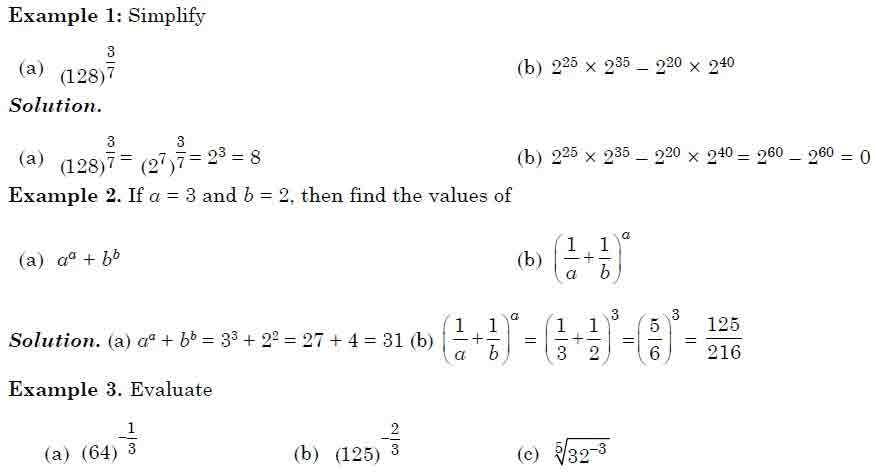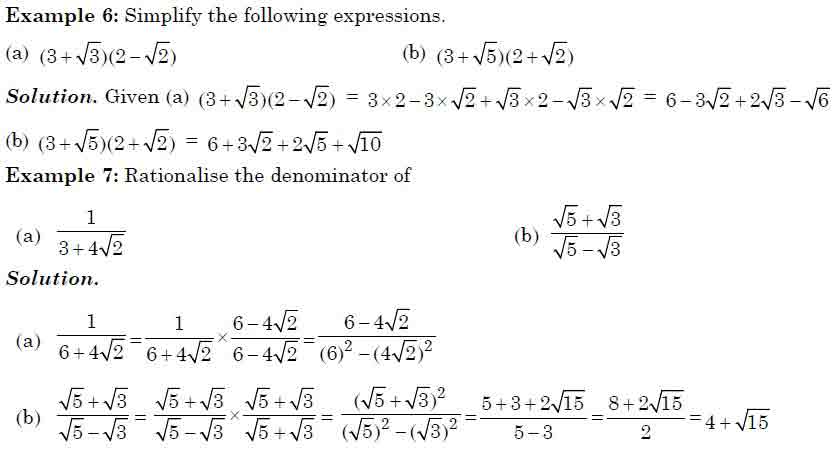(HOT) UPSC Current Affairs 2025 PDF
NEW! The Gist (NOV-2025) | E-BOOKS
(Online Course) CSAT Paper - II : Basic Numeracy: Indices and Surds
Basic Numeracy
Indices and Surds
In our day-to-day life, we get plenty of data in form of powers of numbers. To have a feeling of what they measure we need to have an exact idea of indices and surds. There may be some kit items in CSAT, specifically designed to test proficiency of candidates in indices and surds.
Indices
In the expression xn, n is called the exponent or index and x is called the base and xn is read as ‘x to the power of n’ or ‘x raised to the power n’.
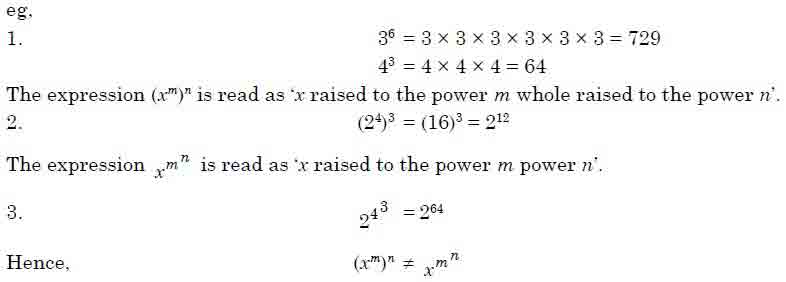
Laws of Indices
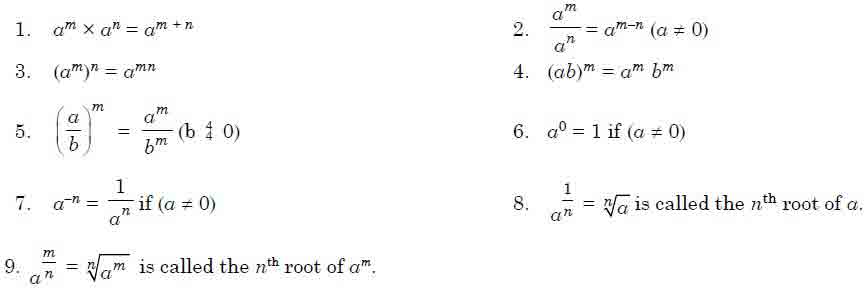
10. When the bases of two numbers are equal, then their powers are also equal.
eg, If 3n = 32, then, n = 2.
11. When the powers of two numbers are equal, then their bases are equal.
eg, If a3 = 43, then a = 4.
Where a is a positive real number and n is a rational number.
Surds

Laws of Radicals

Rationalisation of a Surd
If the product of two surds is rational, then each of the two surds is called
a rationalising factor of the other. In general if the surd is of type
![]() ,
then its rationalising factor is a
,
then its rationalising factor is a
![]() .
.
The rationalising factor of a surd is not unique. But it is always convenient to
use the simplest of all rationalising.
Factors of a given Surd

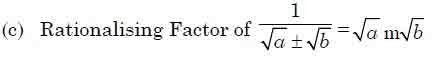

Comparison of Surds
Comparison of surds is possible only when they are of the same order. The radicals can be compared.