(IGP) IAS Pre Paper - 2: GS - Basic Numeracy - Time & Distance

Relation between Time, Speed and Distance

Distance covered, time and speed are related by

Time = Distance/Speed                                         ...(i)

Speed = Distance/Time                                         ...(ii)

Distance = Speed × Time                                     ...(iii)

• Distance is measured in meters, kilometers and miles.
• Time in hours, minutes and seconds.
• Speed in km/h, miles/h and m/s.

1. To convert speed of an object from km/h to m/s multiply the speed by 5/18

2. To convert speed of an object from m/s to km/h, multiply the speed by 18/5

Average Speed

It is the ratio of total distance covered to total time of journey.

Average speed = Total distance covered/Total time of journey

General Rules for Solving Time & Distance Problems

Rule 1

If a certain distance is covered with a speed of ‘x’ km/h and another equal distance with a speed of ‘y’ km/h, then the average speed for the whole journey is the harmonic mean of the two speeds.

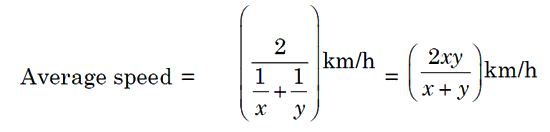
Rule 2

If three equal distances are covered by three different speeds x, y and z km/h, then average speed for the whole journey is given by

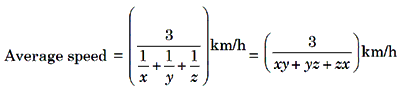
Rule 3

If a certain distance is covered with a speed of ‘x’ km/h and another distance with a speed of ‘y’ km/h but time interval for both journeys being same, then average speed for the whole journey is given by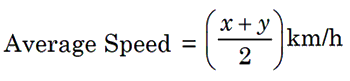

Rule 4

If a certain distance is covered with a speed of x, y and z km/h, but time inverval for the three journey being equal, then average speed is given by

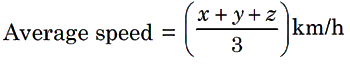
Rule 5

If the ratio of speeds A and B is x : y, then the ratio of times taken by themto cover the same distance is 1/x: 1/y

Relative Speed

(i) If two bodies aremoving in the same direction at x km/h and y km/h, where (x> y), then their relative speed is given by (x – y) km/h.
(ii) If two bodies are moving in opposite direction at x km/h and y km/h, then the their relative speed is given by (x + y) km/h.

General Rules for Solving Train Problems

Rule 1 Train Vs Stationary Object of no Length

Time taken by a train of length ‘l’metre to pass a stationary object such as a pole, standingman or a building is equal to the time taken by the train to cover l metre.

Speed of the train = Length of the train/Time taken to cross the stationary object

Rule 2 Train Vs Stationary Object of Certain Length

Time taken by a train of length ‘l’ metre to pass a stationary object of length ‘a’ metre such as another standing train, bridge or railway platform is equal to the time taken by the train to cover (l + a) metre.

Speed of the train = Length of the train+Lengthof the stationary object/Time taken to cross the stationary object

Rule 3 Train Vs Moving Object of no Length

Time taken by the train of length ‘l’ metre to pass a man moving is equal to the time taken by the train to cover l metre
(i) When the train and man move in the same direction with speeds of x m/s and y m/s. Then,

(x – y) = Length of the train/Time taken to cross each other

(ii) When the train and man move in opposite directions with speeds of x m/s and y m/s. Then,

(x + y) = Length of the train/Time taken to cross each other

Rule 4 Train Vs Moving Object of Certain Length

Time taken by the train of length ‘l’ metre to pass amoving object of length ‘a’ metre such as another moving train is equal to the time taken by the train to cover (l + a) metre.
(i) When the two trains move in the same direction with speeds of x m/s and y m/s, (x > y), then

(x – y) = Length of the train + Length of train two/ Time taken to cross each other

(ii) When the two tains move in opposite directions with speeds of x m/s and y m/s. Then,

(x + y) = Length of the train one + Length of train two/Time taken to cross each other

Rule 5 Two Moving Train

If two trains start at the same time frompoints A and B towards each other and after crossing they take a and b second in reaching B and A respectively. Then, (A’s speed) : (B’s speed) = Öb : Öa .

General Rules for Solving Boats and Streams Problem

Downstream Motion

When an object is moving against (opposite) direction in which the water in the stream is flowing, then the object is said to be moving upstream.

Upstream Motion

When an object is moving against (opposite) direction in which the water in the stream is flowing, then the object is said to be moving upstream.

Mot ion in Still Water

When an object is moving in water where there is no motion in water, the object can move in any direction with a uniform speed, then the object is said to be moving in still water.

Rule 1 Downstream and Upstream Speed

Let the speed of the boat in still water = x km/h and speed of the stream be y km/h, then
Speed of the boat with stream downstream speed = (x + y) km/h
Speed of the boat against stream = upstream speed = (x – y) km/h
As, when the boat is moving downstream, the speed of the water aids the speed of the boat and when the boat is moving upstream, the speed of the water reduces the speed of the boat.

© UPSCPORTAL.COM