Work to be done is generally considered as one unit. It may be digging a trench constructing or painting a wall, filling up or emptying a tank, reservoir or a cistern.

General rules to be followed in the problems on Time and Work

1. If Acan do a piece of work in n days, then work done by A in 1 day is 1/n. ie, if a person can do some work in 12 days, he does 1/ 12th of the work in one day.

2. If A s 1 day’s work = 1/n, then A can finish the whole work in n days. ie, if a person’s one day work is 1/10, then he can finish the whole work in 10 days.

3. If A is thrice as good a workman as B, then ratio of work done by A and B = 3 : 1. ie, if a man works three times as fast as a woman does, then when the work is complete, 3 parts of the work has been done by the man and 1 part by the woman.

4. If A is thrice as good a workman as B, then ratio of time taken by A and B = 1 : 3. ie, if the woman takes 15 days to complete the work, then the man takes 5 days to complete the same work.

5. If two persons A and B can individually do some work in a and b days respectively, then A and B together can complete the same work in ab (a + b) days.

6. The fundamental rules on variation also apply in Time and Work.
(i) Work and men are directly proportional to each other ie, if the work increases, the no. of men required to do it, also increases, if the work is to be completed in the same number of days.
(ii) Men and days are inversely proportional, ie, if the number of men increases, the number of days required to complete the same work decreases and vice versa.
(iii) Work and days are directly proportional, ie, if the work increases, the number of days required also increases, if the work is to be completed with the same number of men and vice versa.

Example 1: Ravi can do a job 10 days. Determine his one day job.
Solution. Ravi’s 10 days work = 1

Ravi’s 1 day work = 1/10

Example 2: Tuktuki and Rasmani can do a job alone in 20 days and 30 days respectively. In how many days the job will be finished, if they work together.

Example 3: Mary and Maurice can do a piece of work in 10 days and 15 days respectively. They work together for 3 days and then Maurice leaves. Mary finishes the remaining work alone. In how many days in the total work finished?

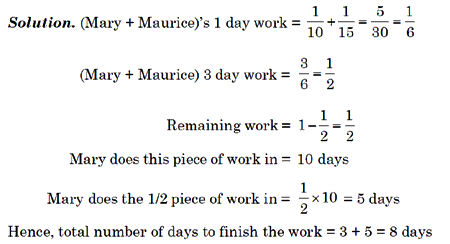
Example 4: Ravi and Rishi can do a piece of work in 24 days, Rishi and Ronit in 30 days, Ronit and Ravi in 40 days. In how many days will they finish it together and separately?
Solution. (Ravi and Rishi)’s 1 day’s work =1/24
(Rishi and Ronit)’s 1 day’s work = 1/30
(Ronit and Ravi)’s 1 day’s work = 1/40

On adding, we get
2 (Ravi + Rishi + Ronit)’s 1 day’s work= (1/24 + 1/30 + 1/40) = 1/10
So, (Ravi + Rishi + Ronit)’s 1 day’s work= 1/20
So, they all together can finish the work in 20 days.
Ravi’s 1 day’s work = [(Ravi + Rishi + Ronit)’s 1 day’s work] – [(Rishi + Ronit)’s 1 day’s work]
                                                                        = (1/20 – 1/30) = 1/60
So, Ravi alone can finish the work in 60 days.
Similarly,                     Rishi’s 1 day work= (1/20 – 1/40) = 1/40
So, Rishi alone can finish the work in 40 days
And                            Ronit’s 1 day work = (1/20 – 1/24)
                                                                 = 1/120
So, Rishi alone can finish the work in 120 days.

Example 5: 4 men and 5 women do a piece of work in 8 days while 5 men and 5 women finish it in 6 days. 3 men and 5 women will finish it in how many days?
Solution. (4 men + 5 women)’s 1 day’s work = 1 /8
(5 men + 5 women)’s 1 day’s work 1/6
Subtracting, 1 man’s 1 day’s work = (1 /6 – 1/8) = 1/24
(3 men + 5 women)’s 1 day’s works = (1 /8 – 1/24) = 1/12
Thus, 3 men and 5 women will finish it in 12 days.

Pipes and Cisterns

A pipe or a tap connected with a tank (or a cistern or a reservoir) is called an inlet, if it fills it.
A pipe or a tap connected with a tank (or a cistern or a reservoir) is called an outlet, if it empties it.

General rules to be followed in the problems on Pipes and Cisterns

1. If a pipe can fill a tank in a hour, then the part filled in 1 h = 1 /a
2. If a pipe can empty a tank in b hour, then the part of the full tank emptied in 1 h = 1 / b
3. If a pipe can fill a tank in a hour and another pipe can empty the full tank in b hour, then the net part filled in 1 h, when both the pipes are opened
= (1/a – l/b)

Thus, in Pipes and Cisterns a filling pipe or tap does positive work and an emptying pipe or a leak does negative work.

Example 6: A pipe can fill 4 of cistern in 12 min. In how many minutes it fill 1/2 of cistern.
Solution. QTime taken to fill 3/4 of cistern
                                        = 12 min

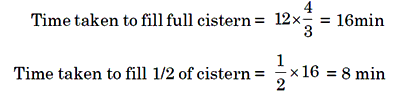
Example 7: A tap can fill a cistern in 20 min and another tap can fill in 30 min. If both are opened simultaneously, find the time when the cistern will be full.
Solution. Total part that can be filled in 1 min 1/20=1/30=1/2
Tank will be filled in 12 min.

Example 8: Pipe A can fill a tank in 15 min, pipe B in 18min and a leak can empty the tank in 90min. If all of them work together, find the time taken to fill the empty tank?
Solution. Net part filled in 1 min = (1/15 + 1/18 – 1/90) = 1/9
So, the empty tank will be filled in 9 min.

Example 9: Two taps A and B can fill a tank in 20 and 40 min respectively. Both the taps are opened and after 10 min tap A was shut. In how much more time will the tank be full?
Solution. Part filled by (A+ B) in 10 min = 10 (1/20 + 1/40) = 10×3/40 = 3/4
Part of the tank to be filled = (1–3 /4) = 1/4
Now, 1/4th of the tank can be filled by B in (1/4)×40 = 10 min
So, the tank would be full in 10 more min.