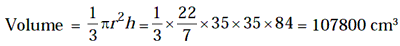(Online Course) CSAT Paper - II : Basic Numeracy: Volume & Surface Area of Solid Figures

Volume & Surface Area of Solid Figures

Solid

Anything that occupies space is calleda Solid. In addition to area, a solid figure has volume also. It has three dimensions namely, length, breadth and height. For solid two different types of areas namely, lateral surface area or curved surface area and total surface area are defined.

1.Prism

A solid having two congruent and parallel faces, called bases and whose other faces, the lateral faces are parallelograms, formed by joining corresponding vertices of the bases is called a Prism.

2. Right Prism

A prismin which bases are perpendicular to the lateral edges is calleda Right Prism. The base of the prism can be a polygon.
In a right prism

(i) Number of lateral surfaces = Number of sides of the base of the prism
(ii) Total number of surfaces of a prism = Number of lateral surfaces + 2
(iii) Lateral surface area = Perimeter of base × Height
(iv) Total surface area = Lateral surface area + 2 (Area of base)
(v) Volume = Area of base × Height

3. Cuboid

A right prism in which the base is a rectangle is called a Cuboid. If l is the length and b the breadth of the base and h the height, then

 

 

Lateral surface area = 2 (l + b)h sq unit
Total surface area = 2(l + b)h + 2lb = 2 (lb + bh + lh) sq unit
Volume = lbh cu unit
The longest diagonal of the cuboid = Öl2 + b2 + h2 unit

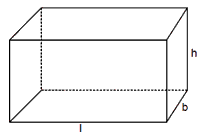
4. Cube

A right prismin which the base is a square and height is equal to the side of the base is alled a cube. If x is the
side of the cube, then lateral surface area = 4x× x = 4x²sq unit
Total surface area = 4x² + 2(x²) = 6x² sq unit
Volume = x² × x = x³ cu unit
The longest diagonal of the cube = Ö3x unit

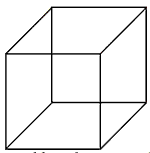
5. Cylinder

If the base of a right prism is circular, then it becomes a cylinder. The lateral surface area c the cylinder is a single curved surface called the curved surface area. If r is the radius of the has and h is the height of the cylinder, then

Curved surface area = 2Πrh sq unit
Total surface area = 2Πrh + 2Πr2 = 2Πr (r + h) sq unit
Volume of cylinder =Πr2h cu unit

 

6. Cone

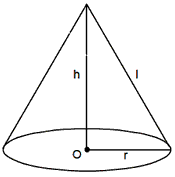
If the base of a right pyramid is circular, then it becomes a cone. The lateral surface area of the cone is a single curved surface. If r is the radius of the base h is the height of the cone and 1 the slant height of the cone,

then slant height, l =Öh2 + r2 unit
Curved surface area = Πrl sq unit
Total surface area = Πrl+ Πr2= Πr (l+ r) sq unit
Volume of cylinder =1/3 Πr2h cu unit.

7. Frustrum of a Cone

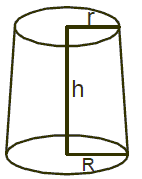
If a cone is cut parallel to base at a hight h then the remaining part is called the frustrum of the cone. If radius of base and vertex of the frustrum of a cone be R and r respectively and height and slant height of it be h and l then

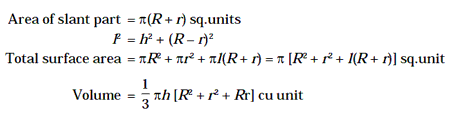
8. Sphere

A sphere is a solid in which any point on the surface of sphere is equidistant from the centre of the sphere.

Surface area = 4Πr² sq unit
Volume =4/3Πr³ cu unit

9. Hemisphere

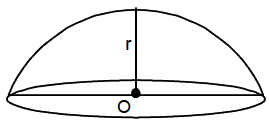
When a sphere is cut into two equal halves, each half is an hemisphere in which the base is circular with radius r and height is equal to the radius.

Curved surface area = 2Πr² sq. unit
Total surface area = 2Πr²+Πr²sq. unit = 3Πr² sq. unit
Volume = 2Πr³ cu unit
1 L = 1000cm³

 

10. Pyramids

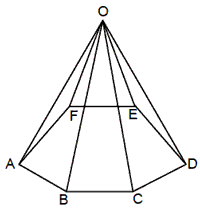
If a point O is joined to the end points of each side of a polygon by straight lines, then it is called a pyramid.

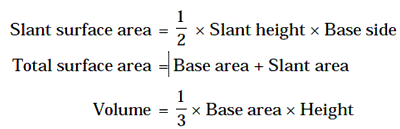
Base area depends on the shape of polygon in the base.
Example 1: Find the volume and total surface area of a cube of side 7 m.
Solution. Here, x =7 m
Surface area = 6 × 2 = (6 × 72) m² = 294 m²
Volume = x³ = (73) m³ = 343 m³

Example 3: Find the length of the longest pole that can be put in a room 15m long, 8m broad and 7m high.
Solution. Here, l = 15 m, b = 8 m and h = 7 m
Required length = Öl2 + b2 + h2 = ( 15)² +(8 )²+ ( 7 )²= Ö388 = 13Ö2 m

Example 4: The length, breadth and height of a room are in the ratio 3 : 2 : 1. The length, breadth and height of the room are increased by 300%, 200% and 100% respectively. Find, how many number of times the volume of the room is increased?
Solution. Let the length, breadth and height of the room are 3x, 2x and x respectively.
Volume of the room = 3x × 2x × x = 6x² After increase
length = 3x + 300% of 3x = 12x
breadth = 2x + 200% of 2x = 6x
height = x + 100% of x = 2x
New volume =12x + 6x + 2x = 144x³
Increase in volume = 144x³– 6x³ = 138x³
Required number of times = 138x³/6x³ = 23 times

Example 5: From a solid sphere of radius 7cm, a right circular cylinderical hole of radius 3 cm and its axis passing through the centre is removed. Find the total surface area of the remaining solid.
Solution. Clearly, height of the cylinder = diameter of the sphere = 14 cm
 

Example 6: The base radius of a cylinder is 14 cm and its height is 30 cm. Find (a) Volume (b) Curved surface area (c) Total surface area
Solution.

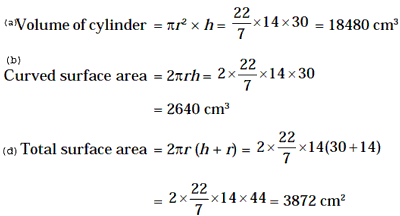
Example 7: How many cubic metres of earth must be dug to make a well 14 m deep and 4 m in diameter?
Solution. Each to be dugout from the well = volume of the cylindrical well =Πr2h = = 176 m3

Example 8: The radius of the base of a right cone is 35 cm and its height is 84 cm. Find
(a) Slant Height (b) Curved Surface Area (c) Total Surface Area (d) Volume
Solution. (a)

(d).