(Online Course) CSAT Paper - II : Logical Reasoning & Analytical Ability: Syllogism

The word ‘Syllogism’ is also referred to ‘Logic’. Syllogism is an important section of logical reasoning and hence, a working knowledge of its rules is required on the part of the candidate. Hence, it can be expressed as the ‘Science of thought as expressed in language’. The questions based on syllogism can be solved by using Venn diagrams and some rules devised with the help of analytical ability. With this unique characteristic, this test becomes an instrument of teaching the candidates to follow the rules and work as per the instructions without an error. Here, only the basic concept and rules, which have a bearing on reasoning faculty could alone help. There are some terminology which are used in syllogism.

Proposition:

It is also referred to as ‘Premises’. It is a sentence which asserts that either a part of, or the whole of, one sets of objects-the set identified by the subject term in the sentence expressing that sentence either is included in, or is excluded from, another set-the set identified by the predicate term in that sentence.

Types of Proposition:

Categorical Proposition There is relationship between the subject and the predicate without any condition.

Example : I. All beams are logs.
                 II. No rod is stick.

Hypothetical Proposition: There is relationship between subject and predicate which is asserted conditionally.

Example : I. If it rains he will not come.
                 II. If he comes, I will accompany him.

Disjunctive Proposition In a disjunctive proposition the assertion is of alteration.

Example : I. Either he is brave or he is strong.
                 II. Either he is happy or he cannot take revenge.

Parts of Proposition:

It consists of four parts.

1. Quantifier: In quantifier the words, ‘all’, ‘no’ and ‘some’ are used as they express quantity. ‘All’ and ‘no’ are universal quantifiers because they refer to every object in a certain set. And quantifier ‘some’ is a particular quantifier because it refers to at least one existing object in a certain set.

2. Subject: It is the word about which something is said.

3. Predicate: It is the part of proposition which denotes which is affirmed or denied about the subject.

4. Copula: It is the part of proposition which denotes the relation between the subject and predicate.
    

For Example:        

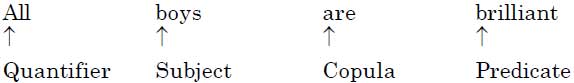
Hence, the standard form of proposition is
Quantifier + Subject + Copula + Predicate

Four-fold classification of categorical proposition: On the basis of quality and quantity of proposition

we can classify them in four categories. To draw valid inferences it is necessary to have a clear
understanding of the A, E, I, O relationship as given in the table.

Rules for Deriving the Conclusions from Two Given Premises

1. Universal affirmative or A-type proposition.

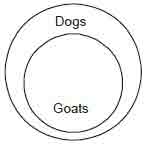
Take an example : All goats are dogs This is A type proposition:We can see it by graphical representation of the above proposition we observe that goats are distributed in dogs. Hence. we can conclude that in A type
proposition only subject is distributed.
2. Universal negative or E-type proposition.

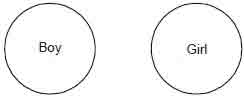
Take an example : No girl is boy In this type of proposition both subject and predicate are denial of each other. This can also be seen in the diagram representing boy Girl and girl. They have nothing in common. Hence, both subject and predicate are distributed.
3. Particular affirmative or I-type proposition.

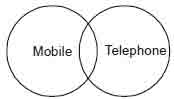
Take an example : Some mobiles are telephones. In this type of proposition subject and predicate have something in common. This implies that in I-type neither subject nor Mobiles Telephones predicate is distributed.We can see it graphically as given in figure.

4. Particular negative or O-type proposition.

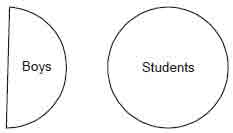
Take an example : Some boys are not students. In O-type propositions some of the category represented by boys subject is not students, whichmeans that a section of boys is deniedwith the entire category of students. It is, therefore, deduced that in O-type proposition only predicate is distributed. On account of different logical approach required to be applied for drawing each type of inference, a clear understanding of this difference becomesmore important.

Rules for Mediate Inference
First introduced by Aristotle, a syllogism is a deductive argument in which conclusion has to be drawn from two propositions referred to as premises. Now consider an example.

Statement: I. Vinay is a boy. II. All boys are honest.
Conclusion I. Vinay is honest.

First two sentences I and II are called propositions and the sentence I is called conclusion. This conclusion is drawn from above given two propositions. Types of Questions Asked in the Examination
There are mainly two types of questions which may be asked under this

1. When premises are in specified form Here premise is in specified form. Here mainly two propositions are given. Propositionsmay be particular to universal; universal to particular; particular to particular; universal to universal.

2. When premises are in jumbled/mixed form Here at least three or more than three proposition are given. Here pair of two propositions out of them follow as same as in specified form.

Type 1 Premises in Specif ied Forms
Case 1: The conclusion does not contain themiddle termMiddle termis the termcommon to both the premises and is denoted byM.Hence, for such case, conclusion does not contain any common termbelong to both premises.

Example 1
Statement: I. All men are girls.
II. Some girls are students.
Conclusions I. All girls are men.
II. Some girls are not students.
Solution. Since, both the conclusions I and II contain the middle term ‘girls’ so neither of them can follow.
Venn diagram Representation: All possible cases can be drawn by using Venn diagram.

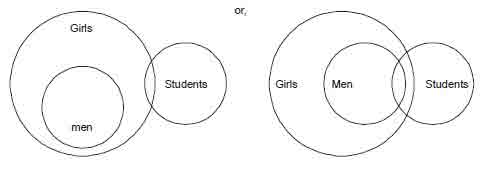
By using both representation (a) and (b) it is clear all girls cannot be men as well as (a) shows some girls are students, here noman is included but at the same time (b) shows some girls are students have somemen are also students as all men are girls. Hence, we cannot deduce conclusion II.
So, neither of them can follow.

Example 2

Statement: I. All mangoes are chairs.
                   II. Some chairs are tables.
Conclusions I. All mangoes are tables.
                    II. Some tables are mangoes.
                    III. No mango is a table.

Solution. Here, the term chair is common to both the statement and hence, is the middle term. Statement (I) is A type proposition and in A-type proposition, only subject is distributed, hence, chair being the predicate in the statement (I) is not distributed in the second statement. Thus, none of the conclusions following statement \is a valid inference.
Venn diagram representation: All possible cases can be drawn as

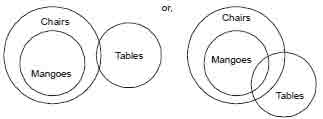
(i) All mangoes are table-this inference is definitely false neither (a) nor (b) shows this conclusion.
(ii) Some tables are mangoes, this inference is uncertain or doubtful.
(iii) No mango is a table, this inference is also uncertain or doubtful. Though it can be concluded fromthe above discussion that no valid inference can be drawn between mango and table.

Case 2: No term can be distributed in the conclusion unless it is distributed in the premises. If case 1 is compiled with by a pair of statement, it is confirmed that valid mediate inferences can be drawn from such pair of statement. But every mediate inference drawn cannot be valid. Therefore, case 2 is applied to check as to the conclusions drawn from a pair of statement in which middle term is distributed, is valid.

Example 3
Statement: I. Some boys are students.
                   II. All students are teenagers.
Conclusions I. All teenagers are students.
                    II. Some boys are teenagers.

Solution. Statement I is an I-type proposition which distributes neither the subject nor the predicate. Statement II is an A type propositionwhich distributes the subject ‘students’. Conclusion I is an A-type proposition which distributes the subject ‘teenagers’ only. Since. the termteenagers is distributed in conclusion Iwithout being distributed in the premises. So, conclusion I cannot follow. In second conclusion, where it is asked that some boys are teenagers. But from statement I it is clear that some students are not students. These students may not be teenagers.

Venn diagram representation: All possible cases can be drawn as follows

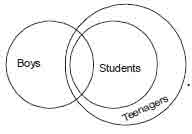
We have given that all students are teenagers so, its reverse cannot be possible. Hence, conclusion I is false. As we are also given that some boys are students and all students are teenagers. So, some boys which are students must be teenagers. Hence, conclusion II follows.

Case 3: If one premises is particular, conclusion is particular. Take an example which explains this case

Example 4
Statement: I. Some boys are thieves.
                II. All thieves are dacoits.
Conclusions I. Some boys are dacoits.
                   II. All dacoits are boys.
Solution. Since, one premise is particular, the conclusionmust be particular. So, conclusion II cannot follow. Venn diagram representation: All possible cases can be drawn as follows

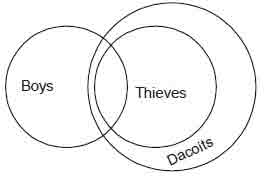
Here conclusion I follows but the conclusion II cannot follow.

Case 4 : If the middle term is distributed twice, the conclusion cannot be universal Take an example which
explains such case.

Example 5
Statement: I. All Lotus are flowers.
                   II. No Lily is a Lotus.
Conclusions I. No Lily is flowers.
                   II. Some Lilies are flowers.

Solution. Here, the first premise is an A proposition and so, the middle term ‘Lotus’ forming the subject is distributed.The second premise is an E proposition and so, the middle term ‘Lotus’ forming the predicate is distributed. Since, the middle term is distributed twice, so the conclusion cannot be universal.

Venn-diagram representation: All possible cases can be drawn as follows

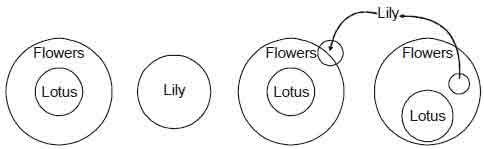
It is clear from the given Venn-diagrams either conclusion I or II must be followed.

Case 5 If both the premises are affirmative, the conclusions must be affirmative. Take an example which follows such case:

Example 6
Statement: I. All gardens are schools.
                  II. All schools are colleges.
Conclusions I. All gardens are colleges.
                  II. Some gardens are not colleges.

Solution. Since, both the premises are affirmative, the conclusion must be affirmative, so conclusion II cannot follow.
Venn diagram representation: All possible cases can be drawn as follows.

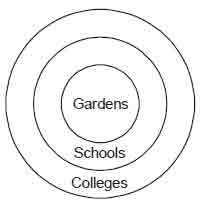
Now, taking conclusion I, it is clear that all gardens are also colleges. But taking conclusion II, we cannot that derive second conclusion is true. Hence, only the first conclusion must be true.

Case 6 No conclusion follows. There are three types of such cases.
(a) If both the premises are particular

Example 7
Statement: I. Some cups are spoons.
                  II. Some spoons are sauccers.
Conclusions I. All cups are sauccers.
                    II. Some sauccers are cups.
Solution.Since both the premises are particular, so no definite conclusion follows.

Venn diagram representation

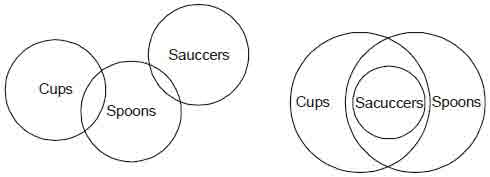
It is clear from both given Venn-diagrams that no conclusion is followed.
(b) If both the premises are negative

Example 8
Statement: I. No flower is mango.
                  II. No mango is cherry.
Conclusions I. No flower is cherry.
                    II. Some cherries are mangoes.

Solution. Since, both the premises are negative hence, neither conclusion follows.
(c) I f the major premise is particular and the minor premise is negative
Major premise is the predicate of the conclusion andminor premise is the subject of the conclusion.

Example 9
Statement: I. Some pubs are cows.
                II. No kitten are pubs.
Conclusions I. No pubs are kitten.
                    II. Some cows are kitten.

Solution. Here, the first premise containing themiddle term‘Kitten’ as the subject is themajor premise and the second premise containing the middle term ‘Kitten’ as the predicate is the minor premise. Since, the major premise is particular and the minor premise is negative. So, no conclusion follows.

Venn diagram representation: All possible cases are given

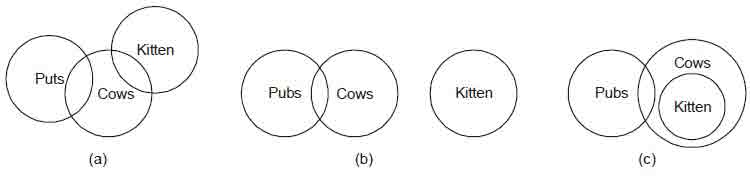
It is clear from the Venn-diagram representation that conclusion I follows. Complementary pair of conclusions
In drawingmediate inferences from given statement, students are required to bemore attentive in selecting complementary pair of conclusion where neither of the conclusions is definitely true but a combination of both makes a complementary pair. As we have already discussed in case number 1 that in the statement wheremiddle term is not distributed, no valid mediate inference can be drawn but there still exists a possibility that a complementary pair of conclusions follows from the statement.

Example 10
Statements I. Some cameras are radios.
                 II. Some statues are cameras.
Conclusions I. Some ratios are statues.
                    II. No radio is statue.

Solution. Either ‘some radios are statues’ or ‘No radio is statue’ follows, as I and E-type proposition form a complementary pair.

Venn diagram representation We can draw all possible cases as given below

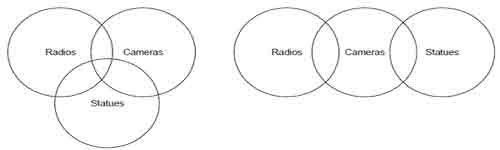
Hence, using both diagrammatical representationwe can conclude either some radios are statues or ‘no radio’ is statue. Hence, at least one of the conclusions must be true.

Special Cases

Facts

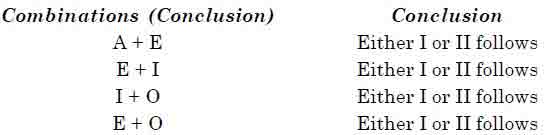
Example 11

Statements I. All vegetables are green.
                    II. Some greens are fruits.
Conclusions I. Some fruits are vegetables.
                    II. No fruit is vegetable.
Solution.     Here, conclusion I is particular affirmative and conclusion II is universal negative proposition.
Hence, either conclusion I or conclusion II follows.
Alternatives

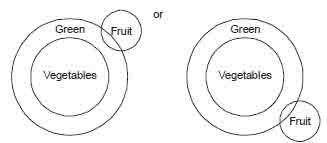
Conclusion: If we follow Venn-diagram (a) then we can say no fruit is vegetable. Conclusion II but if we that follow Venn diagram (b) then we can say some fruits are vegetables (conclusion I).
Here, either Venn diagram (a) or Venn-diagram (b) is possible. Hence, conclusion I or conclusion II must be followed.
Minimal Possibilities We can represent statements by keeping in mind our conclusions It’ we follow that our two conclusions belong to special case, then either one of them is true. We can represent minimum possibilities as given directly in the statement, we don’t need to think about parameters.

Example 12
Statements I. Some fruits are vegetables.
                II. Some vegetables are junk food.
                III. Some junk foods are snacks.
Conclusions I. Some junk foods are vegetables.
                    II. Some junk foods are fruits.
Solution. Minimal possibilities

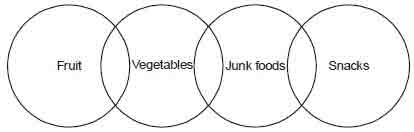
It is clear from the above diagrams that only conclusion I follows.

Type 2 Mixed/jumbled Problems
In such type of problem there is a constitution of mixed problems of universal and particular premises. Directions (Q. Nos. 13 to 16) In each of the questions given below there are three statements followed by three conclusions numbered I, II and III, you have to take the given statements to be true even if they seemto be at variance fromcommonly known facts. Read all the conclusions and then decide which of the given conclusions logically follows fromthe given statements disregarding commonly known, facts.

Example 13
Statements All halls are tyres.
                    Some tyres are wheels.
                    All wheels are cars.
Conclusions I. Some cars are wheels.
                    II. Some cars are tyres.
                    III. Some wheels are halls.

(a) None follows
(b) Only I follows
(c) Only I and II follow
(d) Only III follows

Solution. (c)
Conclusions

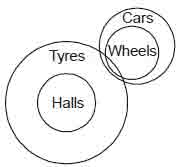
I. Some cars are wheels. It can be seen from Venn-diagram.
II. Also, some cars are tyres (as shown in Venn-diagram).
III. It is not clear from the Venn-diagram. Hence, only I and II follow.

Example 14
Statements Some pictures are frames.
                   Some frames are idols.
                   All idols are curtains.
Conclusions I. Some curtains are pictures.
                    II. Some curtains are frames.
                    III. Some idols are frames.
(a) Only I and II follow
(b) Only II and III follow
(c) Only I and III follow
(d) All follow

Solution. (b)

Conclusions

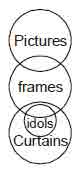
I. Does not follow.
II. Follows (clear from the Venn-diagram)
III. Follows (clear from the Venn-diagram)
Hence, only II and III follow.

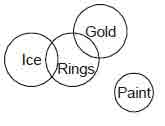
Example 15
Statements Some ice are rings.
                    No ring is paint.
                    Some rings are gold.
Conclusions I. No gold is paint.
                    II. No ice is gold.
                    III. Some rings are paints.
                    IV. All golds are rings.
(a) Only I and III follow
(b) Only I and II follow
(c) Only III and IV follow
(d) None follows

Solution. (d) Hence, none of the conclusions follows.

Example 16
Statements No candle is bell.
                    Some shoes are bells.
                    All tables are shoes.
Conclusions I. Some tables are bells.
                    II. No table is bell.
                    III. Some shoes are candles.
                    IV. No shoes are candles.
(a) Only I and IV follow
(b) Only I and II follow
(c) Only III and IV follow
(d) None of these
Solution. (d)

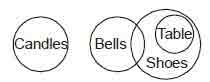
Solution. (d) Here conclusion I is particular affirmative and conclusion II is its universal negative. Hence, either conclusion I or II follows. Also conclusion III is particular affirmative and conclusion IV is its universal negative.Hence, either III or conclusion IV follows. Finally, either conclusion I or II follows and either conclusion III or conclusion IV follows.