(HOT) UPSC Current Affairs 2025 PDF
NEW! The Gist (NOV-2025) | E-BOOKS
(Online Course) CSAT Paper - II : Basic Numeracy: Ratio & Proportion
Basic Numeracy
Ratio & Proportion
Ratio
The ratio of two quantities a and b is the fraction a/b and is expressed as a : b. Here a is the first term or antecedent and b is the second term or consequent. Since the ratio expresses the number of times one quantity contains the other, it is an abstract (without units) quantity.
A ratio remains unaltered if its numerator and denominator are multiplied or divided by the same number. eg, 4 : 3 is the same as (4 × 10) : (3 × 10) ie, 40 : 30.
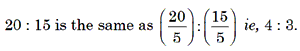
“A ratio is said to be a ratio of greater or less inequality or of equality according as antecedent is greater than, less than or equal to consequent”.
- If a > b, then a : b is called a ratio of greater inequality (eg, 4 : 3, 5 : 2, 11 : 3, ...)
- If a < b, then a : b is called a ratio of less inequality (eg, 3 : 4, 2 : 5, 3 : 11, ...)
- If a = b, then a : b is called a ratio of equality (eg, 1 : 1, 3 : 3, 5 : 5, ...) From this we find that
(i) If a > b and some positive number is added to each term of a : b,
then the ratio is diminished.
If a > b, then (a + x) : (b + x) < a: b.
(ii) If a < b and some positive number is added to each term of a : b,
then the ratio is increased.
If a < b, then (a + x) : (b + x) < a : b.
(iii) If a = b and some positive number is added to each term of a :
b, then the ratio is unaltered. If a = b, then
(a + x) : (b + x) = a : b
Kinds of Ratios
Duplicate Ratio: a2 : b2 is called duplicate ratio of a : b.
Triplicate Ratio: a3 : b3 is called triplicate ratio of a : b.
![]()
Compound Ratio : ab : cd is the compound ratio of a : c and b : d. It is the ratio of the product of the antecedents to that of the consequents of two or more given ratios.
![]()
![]()
Proportion
When two ratios are equal, they make a proportion. ie, if a/b=c/d then a, b, c and d are in proportion. This is represented as a : b : : c : d and is read as “a is to b as c is to d”.
When a, b, c and d are in proportion, then a and d are called the Extremes and b and c are called the Means. also, Product of the Means = Product of the Extremes ie, be = ad.
Continued Proportion
If three quantities a, b and c are such that a : b : : b : c, then b2 = ac and a, b and c are in continued proportions. Also, the quantity c is called the third proportion of a and b.
Fourth Proportion
If four quantities a, b, c and x are such that a : b : : b : c, then ax = be and x is called the fourth proportion of a, b, and c.
Mean or Second Proportion
If three quantities a, b and x are such that a : x : : x : b, then x2 = ab
and x is called the mean of a and b. Also, If a : b = c : d, then the following
properties hold good.
(i) b : a = d : c (Invertendo)
(ii) a : c = b : d (Alter nendo)
(iii) (a + b) : b = (c + d) : d (Componendo)
(iv) (a – b) : b = (c – d) : d (Dividendo)
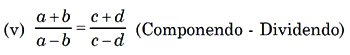
Variation
If two quantities x and y are related in such a way that as the quantity x changes it also brings a change in the second quantity y, then the two quantities are in variation.
Direct Variation
The quantity x is in direct variation to y if an increase in x makes y to increase proportionally. Also a decrease in x makes y to decrease proportionally it can be expressed as x= ky. Where, k is called the constant of proportionality. eg, Cost is directly proportional to the number of articles bought.
Inverse Variation
The quantity x is in inverse variation to y if an increase in x makes y to decrease proportionally. Also, a decrease in x makes y to increase proportionally. It can be expressed as
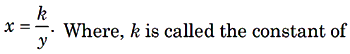 proportionality. eg, The time taken by a vehicle in covering a certain distance
is inversely proportional to the speed of the vehicle.
proportionality. eg, The time taken by a vehicle in covering a certain distance
is inversely proportional to the speed of the vehicle.
Joint Variation
If there are more than two quantities x, y and z and x varies with both y and z, then x is in joint variation to y and z. It can be expressed as x = kyz. Where, k is the constant of proportionality. eg, Men doing a work in some number of days working certain hours a day.
Distribution of an Amount
If an amount A is distributed in the ration a : b, then

Example 2: The ratio of boys to girls in a science class of 28 is 16 :
12. Express it in simplest ration.
Solution. 16 : 12 = 8 : 6 = 4 : 3
Which is the ratio in its simplest form.
Example 3: Compare the ratio of the third proportion of 6 and 5 with
the fourth proportion of 4, 3 and 10.
Solution. Third proportion of 6 and 5 is 6 : 5 : : 5 : x

Example 4: Two numbers are in the ratio 2 : 3. If 10 is added to each,
they are in the ratio 4 : 5. Find the two numbers.
Solution. Let the two numbers be x and y.
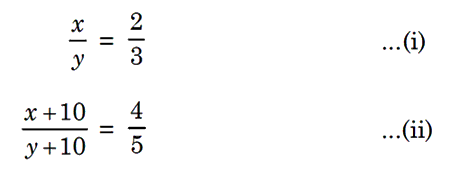
Solving (i) and (ii) we get x = 10 and y = 15
The two numbers are 10 and 15.
Example 5: The ratio between two numbers is 3 : 7. If their LCM is
210, find the numbers.
Solution. Let the numbers be 3x and 7x

