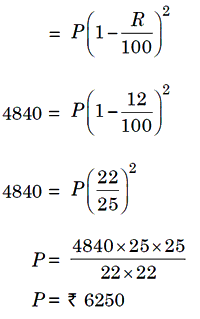(Online Course) CSAT Paper - II : Basic Numeracy: Compound Interest

Compound Interest

In compound interest, the interest is added to the principal at the end of each period and the amount thus obtained becomes the principal for the next period. The process is repeated till the end of the specified time.

If

P = Principal
R = Rate per cent per unit time
Time = n years
A = Amount; CI = Compound Interest

When the interest is compounded annually

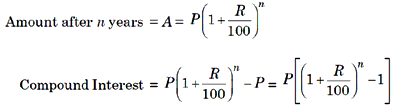
Important Formulae

1. If the rate of interest differs from year to year ie, R₁ in the first year, R₂ in the second year, R₃ in the third

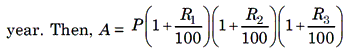
2. When the principa changes every year, we say that the interest is compounded annually. Then,

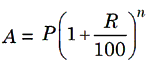
3. When the principal changes as per every six months, we say that the interest is compounded half yearly or semi-annually. Then,

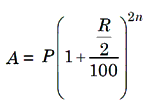
4. When the principal changes every three months, we say that the interest is compounded quarterly. Then

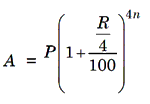
5. When the principal changes after every month, we say that the interest is compounded monthly. Then,

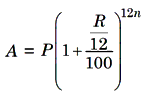
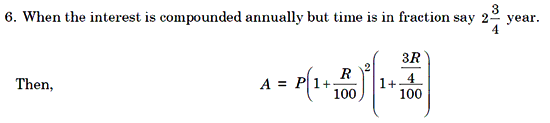
7. The difference between the simple interest and compound interest for 2 year (or terms) is given by the formula

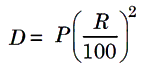
Where D is the difference, P is the principal and R is the rate of interest.

8. Present worth of x Rs. due n years, hence is given by

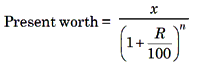
Example 1: Find the compound interest on Rs. 5500 at 9% per annum for 2 year, if the interest is compounded annually?
Solution. P = Rs. 5500, R = 10% per annum and n = 2 year

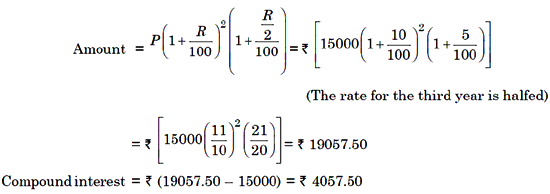
Example 2: Find compound interest on Rs. 12000 for 3 year, if the rate of interest for first year is 5%, second year is 6% and third year is 7%.
Solution: P = Rs. 12000, R₁ = 4%, R₂ = 5% and R₃ = 6%

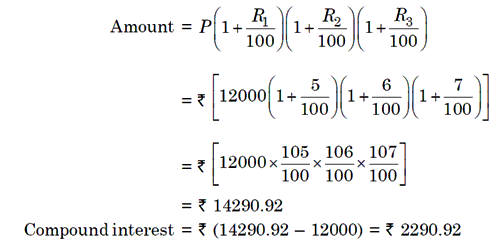
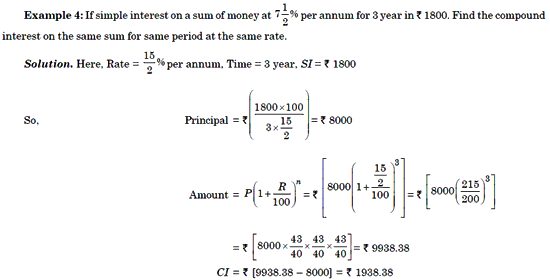
Example 5: The difference between the compound interest and simple interest on a certain sum at 10% per annum for 2 year is Rs. 150. Find the sum.
Solution. Here, D = Rs. 150, T = 2 year, R = 10%

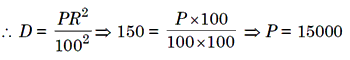
Example 6: In what time will Rs. 64000 invested at 5% per annum fetch an interest of Rs. 4921, the interest being compounded half yearly.

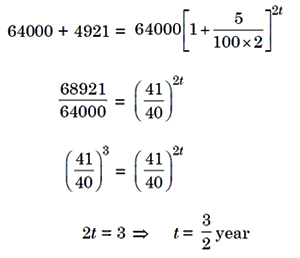
Example 7: The value of a TV that was purchased in January 1999, depreciates at 12% per annum. If its value in January 2001 is Rs. 4840, then what was the purchase price of TV?
Solution. Let P be the price of TV in January 1999, then the value of TV in January 2001, ie, after two years.