(Online Course) CSAT Paper - II : General Mental Ability: Mathematical Operations

The basic approach for the problems of this type is more or less similar to that of coding and decoding. One has to study the symbols or the geometrical figures and their meanings carefully. Then, the meanings are to be used in place of those symbols in answering the questions. The questions can be categorized into two types

Symbols and Notations

Symbols for these types of questions stand for mathematical operations like +, –, ×, ÷, > , <, ³, £, = and #. So, the students must replace the symbols bymathematical operations and apply the BODMAS’ rule to find the value f the given expression. Other symbols which can be used are DÑ, *, @, $, etc, with proper definitions. Some examples are given below

Example 1: If ‘+’ means ‘–’, ‘–’ means ‘×’, ‘×’ means and ‘means’ ‘÷’, and ‘÷’ mean ‘+’ then 15 × 3 ÷ 15 + 5 – 2 = ?
(a) 0
(b) 10
(c) 20
(d) 6
Solution. (b) 15 × 3 = 15 + 5 – 2
after changing the signs = 15 = 3 + 15 – 5 × 2 = 5 + 15 – 10 =10

Example 2: If 2 * 3 = 12, 3 * 4 = 20 and 4 * 5 = 30, then 2 * 6 is
(a) 18
(b) 12
(c) 21
(d) None of these
Solution. (c) The numbers on both sides of * are increased by one and then multiplied to get the answer. 2*6 = 3 × 7 = 21

Example 3: If x $ y = (x + y + xy –1) (x + y + xy + 1), then the value of (4 $ 10) is.
(a) 2915
(b) 2195
(c) 2951
(d) 2955
Solution. (a) As per the definition of $, (4$10) would be (4 + 10 + 4 × 10 - 1) (4 + 10 + 4 × 10 + 1) = 2915. So,
answer is (a)

Example 4: If* means “is greater than”, @ means `is less then’; and $ means “is equal to” and if a $ b and b @ c, then
(a) c * b
(b) b * c
(c) c * a
(d) Both (a) and (c)
Solution. (d) Replace the symbols with the meaning given against them. If a $ b and b @ c would become a = b and b < c, then c > b or c > a ie, c * b, c * a are true from the given options.

Geometrical Figures

These figures will be divided and subdivided into a number of parts, each part is filled with a number or a letter except one part. The numbers or the letters in the figures follow certain pattern. The objective is to identify the pattern and find themissing number or letter. The problems based on geometrical figures are of various types.

Type 1

Based on circles: In these type of, three circles with numbers outside the circle will be given.In the first two circles, the number inside the circle is written according to a particular pattern. The objective of the student is to find the missing number of third circle.

Example 5:

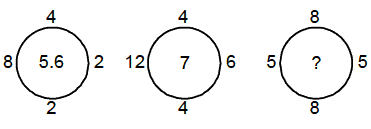
(a) 7.16
(b) 9.25
(c) 6.23
(d) 8.33
Solution. (a) ÖTop number + Bottom number + ÖLeft number + Right number gives the number inside the circle

Ö8 + 8 + Ö5 + 5 = Ö16 + Ö10 = 4 + 3.16 = 7.16

Example 6:

 
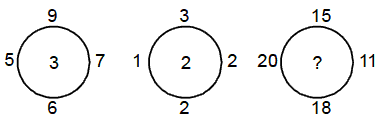
(a) 14
(b) 10
(c) 6
(d) 4
Solution. (d) Cube root of the sum of the numbers outside the circle given the number inside the circle
³Ö(20 +15 +11) = ³Ö64 = 4

Type 2

Circle divided into parts: In such questions, circle is divided into three parts. An arithmetic operation on the numbers gives the missing number.

Example 7:

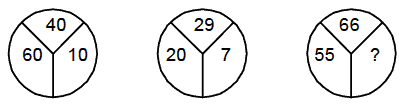
(a) 2
(b) 11
(c) 33
(d) 44
Solution.
(b) 60 + 40 = 10, 20 + 29 = 7
The missing number is 55 + 66 = 11

Example 8:

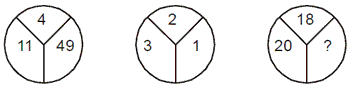
(a) 9
(b) 6
(c) 8
(d) 4
Solution. (d) (11 – 4)2 = 49, (3 – 2)2 = 1
The missing number is (20 – 18)2 = 4

Type 3

Problems based on triangles: In such questions, three triangles are givenwith numbers inside and outside. The number inside the triangle is obtained by operating some arithmetic operators on the numbers outside the triangle.

Example 9:

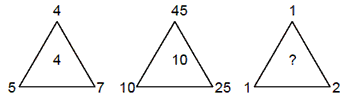
(a) 2
(b) 1
(c) 0
(d) None of these
Solution. (b) (5 + 7 + 4) ÷ 4 = 4
The missing number is (1 + 2 + 1) ÷ 4 = 1.

Example 10:

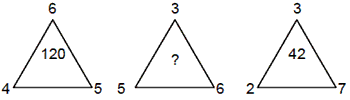
(a) 70
(b) 80
(c) 90
(d) 1
Solution. (c) (4 × 5 × 6) = 120.
The missing number is (5 × 6 × 3) = 90

Type 4

Problems based on squares: Such questions consist of three squares with five numbers inside the square of the 5 numbers, 4 numbers are at the four corners of the square and one middle number follow some arithmetic operation.

Examples 11:

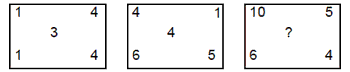
(a) 4
(b) 6
(c) 5
(d) 7
Solution. (c) Ö1 + 1 + 3 + 4 = 3, Ö1 + 4 + 5 + 6 = 4
The missing number = Ö4 + 5 + 6 + 10 = 5

Type 5

Problems based on matrix: In such questions, a square divided into nine parts, three rows and three columns, out of the nine parts, eight parts are filled with one part left vacant. The students need to apply some arithmetic operation to find out the missing number.

Examples 12:

(a) 8
(b) 9
(c) 13
(d) 12
Solution. (d) (6 + 1) = 7, (4 + 2) = 6, -4 column wise
The missing number = 7 + 5 = 12