(IGP) IAS Pre Paper - 2: GS - Basic Numeracy - Coordinate Geometry

CoordinateGeometry is also called Analytical Geometry. It is that branch of geometry in which we use two numbers called coordinates to indicate the position of a point in a plane.

Cartesian Coordinate System

The horizontal line x´ is called the x-axis and the vertical line y´ oy is called the y-axis and together they arecalled the coordinate axes. The point of intersection of these two axes is called the origin. Let P be any point in a plane. From P draw perpendiculars to the coordinate axes meeting the x-axis in M and y-axis in N. Here, OM(x) is the x-coordinate or absicssa of a point P. Similarly, ON(y) is the y-coordinate or ordinate of point P.

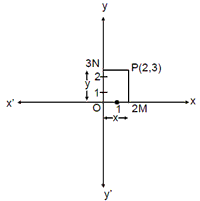
This position of the point P in the plane with respect to the coordinate axes is represented by the ordered pair (x, y) and this system is called the cartesian coordinate system. The coordinates of the origin Oare (0, 0). Also, x´ox and y´oy divide the plane into four regions called quadrants.

1. xoy is quadrant I. Here, x-coordinate is positive and y-coordinate is positive. (+,+)

2. x´oy is quadrant II. Here, x-coordinate is negative and y-coordinate is positive. (–, +)

3. x´oy is quadrant III. Here, x-coordinate is negative and y-coordinate is negative. (–, –)

4. xoy´ is quadrant IV. Here, x-coordinate is positive and y-coordinate is negative. (+, –)

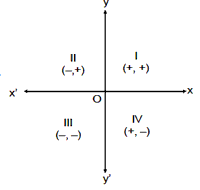
eg,
(1,5) lies in first quadrant (–2,3) lies in second quadrant (–2, –4) lies in third quadrant (4,–2) lies in fourth quadrant The coordinate of origin is (0, 0). The ordinate of every point on x-axis is 0. The ordinate of every point on y-axis is 0. Distance between Two Points: Let P(x_l,y_l) and Q (x₂,y₂) be any two points on the plane, then the distance between P and Q is represented as PQ is given by
PQ = Ö(x₂- x_l)² - ( y₂- y_l )²

The distance of the point P(x, y) from the origin (0, 0) is Öx² + y²
Centroid If A(x_l, y_l) ,B(x₂, y₂) and C(x₃, y₃) are the vertices of a triangle, then the threemedians of the triangle intersect at its centroid and the centroid divides the median in the ratio 2 : 1. A

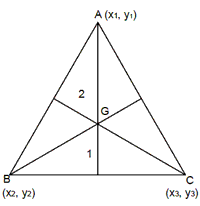
Coordinates of the point G are given by G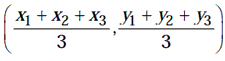
Area of a Triangle: If A(x_l, y_l) ,B(x₂, y₂) and C(x₃, y₃) be three vertices of a triangle ABC, then its area is given by

Collinearity: Three points A(x_l, y_l) ,B(x₂, y₂) and C(x₃, y₃) are said to be collinear, (ie, lying on the same straight line) if
(i) AB + BC= AC or AC+ CB = AB or AB+ AC= BC
(ii) The area of the triangle formed by A, B and C is zero. ie,

x1 (y₂– y₃) + x₂(y₃ – y₁) + x₃(y₁ – y₂) = 0
Section Formula: If A(xl, y1) and B(x2, y2) are two points in a plane, then the coordinates of the point P

which divides the line joining AB internally in the ratio m : n are

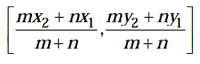
If A(x_l, y_l) ,B(x₂, y₂) be the end points of a line segment AB. Then, the coordinates of the mid point of AB are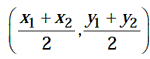

Types of Quadrilaterals

1. Square: If all sides are equal and diagonals are equal.
2. Rhombus: If all sides are equal and diagonals are not equal.
3. Rectangle: If opposite sides are equal and diagonals are equal.
4. Parallelogram: If opposite sides are equal and diagonals are not equal.

The Straight Line

A linear equation of the first degree in two variables x and y represents a straight line. The equation ax + by + c = 0 is the general form of equation of a line. eg,

• 2x + 3y + 6 = 0
• 3y + 5 = 0 [a = 0]. Then, the line is parallel to x-axis.
• 2x + 7 = 0 [b = 0]. Then, the lines is parallel to y-axis.
• 2x + 3y = 0 [c = 0]. Then, the line passes through the origin.

All the above four examples are equations of straight line. The equation of x-axis is y = 0 and equation of yaxis is x = 0.
Slope of Line (m): The slope is the tangent of the angle which the linemakes with the x-axis, in the positive direction. We measure the angle from the x-axis towards the line, in the anti-clockwise direction. The slope m is given as m = tanq°. If q is acute, the slope is positive and if q is obtuse the slope is negative. The slope of a line parallel to x-axis ism = tan0° = 0. The slope of a line perpendicular to x-axis is m = tan 90° = ¥
Slope of a line passing through two points (x1, y1) and (x2, y2) is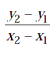

Parallel Lines: Two lines are parallel to each other, if their slopes are equal. Thus, if the slope of line is m, the slope of a line parallel to it is also m. The equation of a line parallel to ax + by + c = 0 is ax + by = k. Perpendicular Lines: Two lines are perpendicular to each other, if and only if the product of their slopes is –1. Thus, if the slope of a line ism, the slope of a line perpendicular to it is -1/m. The equation of a line perpendicular to ax + by + c = 0 is bx – ay = k.

Standard Forms of the Equation of a Line

(i) Slope Intercept Form: The equation of a straight line having slope m and making an intercept c on yaxis is y= mx + c.
(ii) The Two Point Form: The equation of a straight line passing through the points (x₁, y₁) and (x₂, y₂)

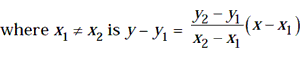
(iii) The Point Slope Form: The equation of a straight line passing through the point (x₁, y₁) and having slope m is y – y₁ = m (x – x₁).
(iv) Double Intercept Form: The equation of a line making intercepts a and b when a ¹ 0 and b ¹ 0 on the x and y axes respectively is x/a + y/b= 1+ = .
(v) The area of a triangle formed by the coordinate axes and the lines having intercepts a and b is ab/2.

Angle between Two Lines

If the angle between two lines of slopes m1 and m2 be q, then

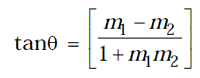
The Circle

(i) The equation of circle whose centre is (h, k) and radius r is given by

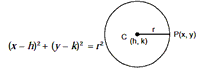
(ii) The equation of circle whose centre is origin and radius r is x² + y² = r².

1. The equationx² + y²+ 2gx + 2 fy + c = 0 represents a circle of radius of Ög² + f ² - c
2. If g² + f ² > 0, then the radius of the circle is real and hence the circle is also real.
3. If g2 + f2 – c = 0, then the radius of the circle is zero. Such a circle is known a point circle.
4. If g2 + f2 – c < 0, then the radius g2 + f 2 - c of circle is imaginary but the centre is real. Such a circle is called an imaginary circle as it is not possible to draw such a circle.
5. Special features of the general equation x2 + y + 2gx + 2fy + c = 0 of the circle are
   • It is quadratic in both x and y.
   • Coefficient of x2 = Coefficient of y2 In solving problems it is advisable to keep the coefficient of x2 and y2 unity.
   • There is no term containing xy ie, the coefficient of xy is zero.
   • It contains three arbitrary constants viz. g, f and c

Example 4: Find the equation of circle whose centre is (–2, 3) and radius is 5. Solution. Required equation of circle is (x + 2)² + (y – 3)²= 5²Þx²+ y²+ 4x – 6y – 12 = 0

Analytical Definition of Conic Section

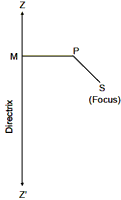
A conic section or a conic is the locus of a point which moves in such a way that its distance froma fixed point always bears a constant ratio to its distance from a fixed line, all being in the same plane. Thus, if S is a fixed point in the plane of the paper and ZZ´ is a fixed line in the same plane, then the locus of a point P which moves in the same plane in such a way that SP/PM = Constant (say) is called a conic section or simply a conic. The fixed point is called the focus of the conic section and the fixed line is known as its directrix. The constant ratio ‘e’ is called the eccentricity of the conic section. z

If e = 1, the conic is called a parabola.
If e < 1, the conic is called an ellipse.
If e > 1, the conic is called a hyperbola.
General Equation of a Conic
Let S(a, b) be the focus, ax + by + c = 0 be the directrix and e be the eccentricity of a conic. Let P(h, k) be any point on the conic such that PM is the perpendicular from P on the directrix. Then, by definition, we have general equation

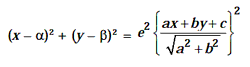
The general equation of the second degree ax² + 2hxy + by² + 2gx + 2fy + c = 0 will represent
(i) a circle, if D ¹ 0, a = b and h = 0
(ii) a parabola, if D ¹ 0, and h² = ab
(iii) an ellipse, if D ¹ 0, and h2 < ab
(iv) a hyperbola, if D ¹ 0, and h² > ab
(v) a rectangular hyperbola, if D ¹ 0 , h² > ab and a + b = 0

Some Useful Terms

• Axis: The straight line passing through the focus and perpendicular to the directrix is called the axis of the conic section.
• Vertex: The point(s) of intersection of the conic section and the axis is (are) called the vertex (vertices) of the conic section.
• Centre The point which bisects every chord of the conic passing through it, is called the centre of the conic section.
• Latus-rectum: The latusrectum of a conic is the chord passing through the focus and perpendicular to the axis.
• Any chord passing through the focus is called a focal chord of the conic section.
• Double Ordinate A chord perpendicular to the axis of a conic is known as its double ordinate.
• if S º ax² + 2hxy + by² + 2gx + 2fy + c = 0, is the equation of a conic, then the coordinates of its centre are

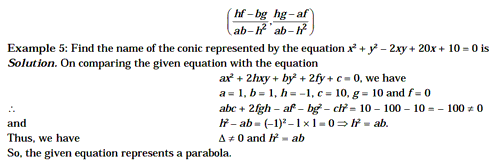
The Parabola

The standard equation of parabola is y² = 4ax

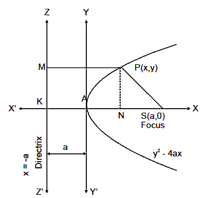
Where (a, 0) is the focus of the parabola.
The parabola has two real foci situated on its axis on of which is the focus S and the other lies at infinity. The corresponding directrix is also at infinity. Some Other Standard Forms of Parabola We find that there are three other standard forms of parabola viz. y² = –4ax, x² = 4ay and x² = – 4ay depending upon the choice of the axes. Thus, in all there are four standard forms. The shapes of the curves in these four standard forms and their corresponding results are as follows.

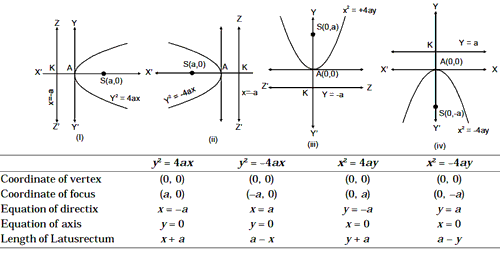
The Ellipse

An ellipse is the focus of a point in a plane which moves in the plane in such a way that the ratio of its distance from a fixed point (called focus) in the same plane to its distance from a fixed straight line (called directrix) is always constant which is always less than unity.

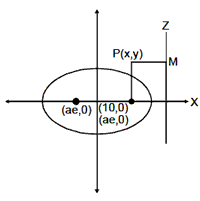
SP/PM = e
Þ SP = e. PM
Equation of Ellipse: The equation of ellipse whose focus is (ae, 0) is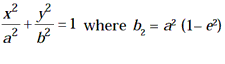

Some Terms Related to an Ellipse

• Vertices: The point A and A, where the curve meets the line joining the foci S and S´, are called the vertices of the ellipse. The coordinates of A and A are (a, 0) and (–a, 0) respectively.
• Major and Minor Axes: The distance AA´ = 2a and BB´ = 2b are called the major and minor axes of the ellipse respectively. Since, e < 1 and b2 = a2 (1 – e2). Therefore, a > b Þ AA´ > BB´
• Foci: The points S(ae, 0) and S´(–ae, 0) are the foci of the ellipse.
• Directrices: ZK and Z´ K´ are two directrices of the ellipse and their equations are x = a/e and x = - a/e respectively.
• Centre Since, the centre of a conic section is a point which bisects every chord passing through it. In case
• Ordinate and Double Ordinate: Let P be a point on the ellipse and let PN be perpendicular to themajor axis AA´ such that PN produced meets the ellipse at P. Then, PN is called the ordinate of P and PNP´ the double ordinate of P.

Hyperbola

A hyperbola is the locus of a point in a plane which moves in the plane in such a way that the ratio of its distance from a fixed point (called focus) in the same plane to its distance from fixed line (called directrix) is always constant which is always greater than unity.

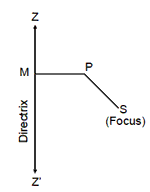
The fixed point is called the focus, the fixed line is called the directrix, the constant ratio is generally denoted by e and is know the eccentricity of the hyperbola.If S is the focus, ZZ´ is the directrix and P is any point on the hyperbola as shown in figure, then by definition,
we have

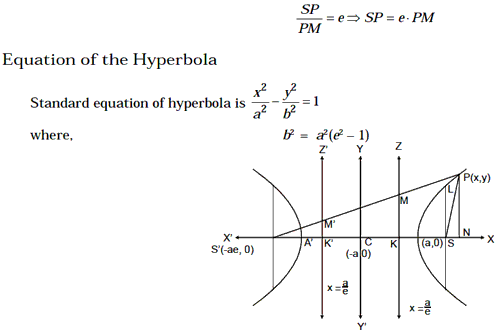
Some Terms Associated to Hyperbola

In this section, we shall define various terms associated to the hyperbola
Vertices The points A and A´, where the curve meets the line joining the foci S and S´, are called the vertices of the hyperbola. The coordinates of A and A´ are (a, 0) and (–a, 0) respectively. Transverse and Conjugate Axes: The straight line joining the vertices A and A´ is called the transverse axis of the hyperbola. Its length AA´ is generally taken to be 2a. The straight line through the centre which is perpendicular to the transverse axis does notmeet the hyperbola in real points. That if B, B´ be the points on this line such that CB = CB´ = b, the line BB´ is called the conjugate axis such that BB´ = 2b.
Foci: The points S (ae, 0) and S’ (–ae, 0) are the foci of the hyperbola.

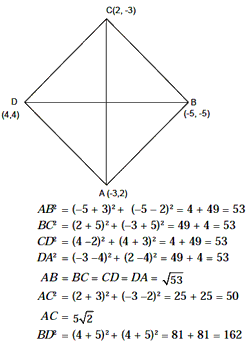
BD = 9Ö2
Diagonal AC ¹ Diagonal BD
Thus, all sides are equal and diagonals are unequal.
ABCD is a rhombus.
Example 9: Find the area of a triangle whose vertices are A(6, – 6), B(3, – 7) and C(3, 3).
Solution. Here, x₁ = 6, y₁ = – 6, x₂ = 3, y₂ = – 7, x₃ = 3 and y₃ = 3

Example 14: Find the ratio in which C(4, – 3) divides the line joining A(1, 3) and B(5, – 5). Solution. Let the required ratio is k : l.
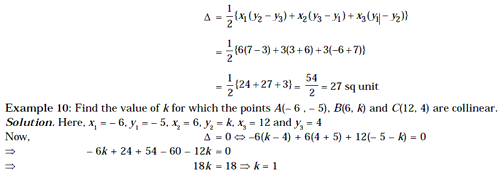
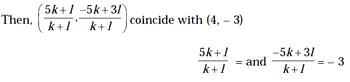
5k + l = 4k + 4l and – 5k + 3l = – 3k – 3l
k = 3l and 6l = 2k Þ k/1 = 3/1 Þ 3 : 1

© UPSCPORTAL.COM