(Paper) CSAT: Basic Numeracy - Sample Questions

Basic Numeracy includes the topics like square roots, factorization, simplification, LCM, HCF, type of numbers, divisibility rules, surds, fractions, polynomials, unit digit calculation, remainder, exponent in factorial, formula based problems, decimal base conversion to binary.

Level of Difficulty-I

1. The number N = 3⁴⁰ + 3⁴¹ + 3⁴² + 3⁴³ is always be divisible by
(a) 2
(b) 3
(c) 5
(d) All of these

2. Number S is obtained by squaring the sum of the digits of a two digit number D. If difference between S and D is 27, then the two digit number D is
(a) 24
(b) 54
(c) 34
(d) 45

Level of Difficulty-II

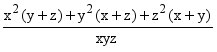
3. If x, y, z are distinct positive real numbers then, would be
(a) greater than 4
(b) greater than 5
(c) greater than 6
(d) none of the above

4. A, B and C are defined as follows
A = (2.000004) ÷ [(2.000004)² + (4.000008)]
B = (3.000003) ÷ [(3.000003)² + (9.000009)]
C = (4.000002) ÷ [(4.000002)² + (8.000004)]
Which of the following is true about the above three expressions?
(a) All three lie between 0.18 and 0.2
(b) A = 2C
(c) C is the smallest
(d) B is the smallest

5. While adding the first few continuous natural numbers, a candidate missed one number of the numbers and wrote the answer as 177. What was the number missed ?
(a) 11
(b) 12
(c) 13
(d) 14

Level of Difficulty-III

6. Consider four digit numbers for which the first two digits are equal and the last two digits are also equal. How many such numbers are prefect squares?
(a) 0
(b) 1
(c) 2
(d) None of the above

7. Let n! = 1 × 2 × 3 × …× n for integer n > 1.
If p = 1! + (2 × 2!) + (3 × 3!) + ….+ (10 × 10!), then p + 2 when divided by 11! leaves a remainder of
(a) 10
(b) 0
(c) 7
(d) 1

8. If x and y are integers then the equation 5x + 19y = 64 has
(a) No solution for x < 300 and y < 0
(b) No solution for x < 250 and y > – 100
(c) A solution for 250 < x < 300
(d) A solution for – 59 < y < – 56