(HOT) UPSC Current Affairs 2025 PDF
NEW! The Gist (NOV-2025) | E-BOOKS
(IGP) IAS Pre Paper - 2: GS - Basic Numeracy - Area of Plane Figures
Basic Numeracy
Area of Plane Figures
Area
The area of a plane figure is the measure of the surface enclosed by its boundary. The area of a triangle or a polygon is the measure of the surface enclosed by its sides.1. Triangle
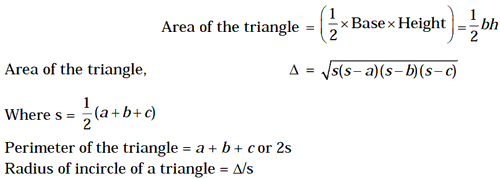
2. Right-Angles Triangle
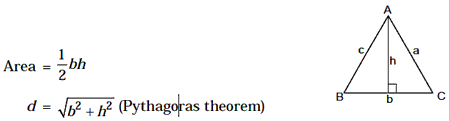
Hypotenuse,
Perimeter = b + d + h
3. Isosceles Right-Angled Triangle
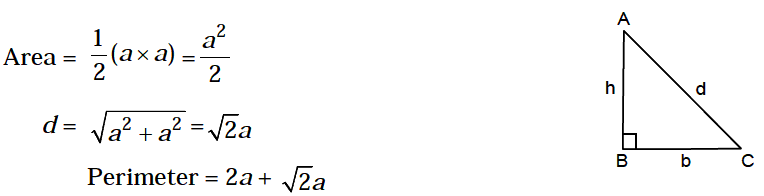
4. Equilateral Triangle
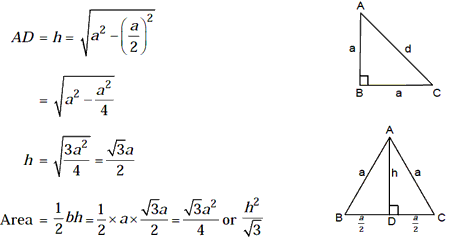
Perimeter = 3a
Radius of incircle of an equilateral triangle of side a = a/2
Ö3
Radius of circumcircle of an equilateral triangle of side a = a/Ö3
5. Square
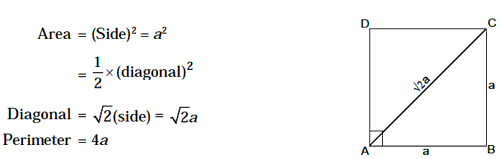
6. Rectangle
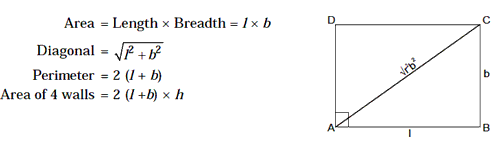
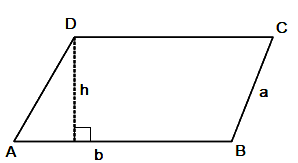
7. Parallelogram
Opposite sides are parallel and equal and opposite angles are equal.
Area = Base × Height = b × h
Perimeter = 2 (a + b)
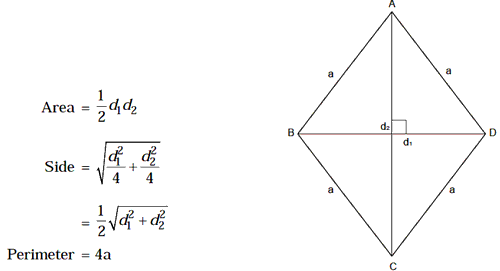
8. Rhombus
All sides are equal and opposite angles are equal. Diagonals bisect each other at right angles.
9. Trapezium
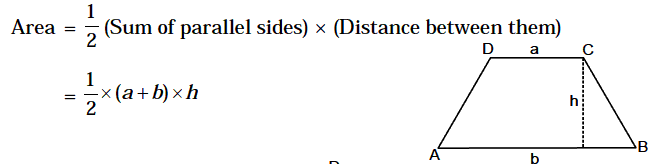
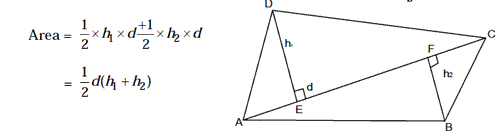
10. Qudrilateral
11. Circle
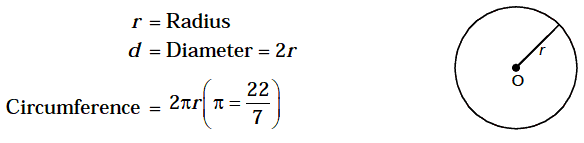
12. Semi-Circle
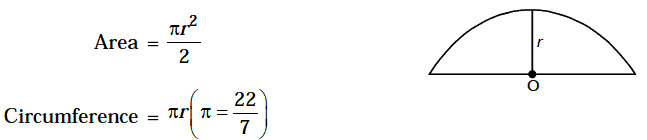
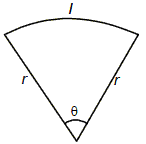
13. Sector
r = Radius, l = Length of the arc
q = Central angle
Area of the sector =1/2 (Arc length* r )= Πr2
q/360
where are length= 2Πrq/360
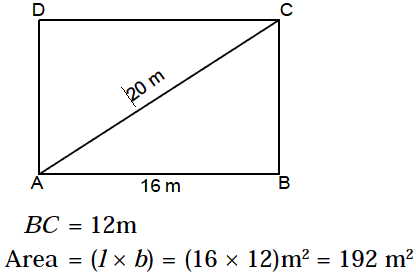
Example 1: One side of a rectangular field is 16 m and one of its
diagonal is 20 m. Find the area of the field. Solution. BC2 = AC2
– AB2 = (20)2 – (16)2 = 400 – 256 =
144
Example 2: The length and breadth of a room are in the
ratio of 3 : 2. Its area is 864 m2. Find its perimeter.
Solution. Let the length be 3x m and breadth be 2x m.
Area = (3x × 2x) = 6x2 = 864= x2 =
144 = x = 12
Length = 3x = (3 × 12) m = 36 m
Breadth = 2x = (2 × 12) m = 24 m
Perimeter = 2 (l + b) = 2 (36 + 24) = 120 m
Solution. r =diameter/2=14/2 = 7m
Area = Πr2=22 /7 *7 *7 =154m2
Circumference = 2Πr == 44m
Example 4:
The areas of two concentric circles are 154m2 and 308m2 respecively. Find
the width of the ring made by them.
Solution. The radius of inner circle r = Ö154/Π
= 7m
Another circle is outside this circle.
If the width of the ring be w then area of the ring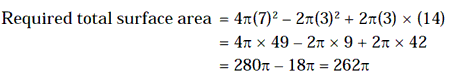
Πw (2r + w) = 308 – 154Example 5: Find the area of a regular hexagon inscribed in a circle whose radius is 15 cm.
22/7*w (14 +w)= 154
w = 289 m
Solution: OC = r = 15 cm
Since, regular hexagon is inscribed in the circle. D BOC is an equilateral triangle
So, BC = a = 15 cm
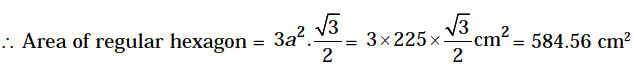
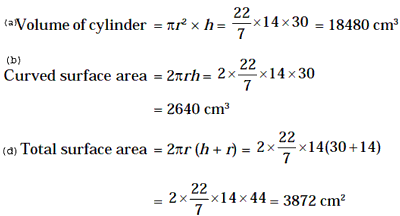
Example 6: A rectangular grassy plot 120m × 80m has a
gravel path 3m wide all round it on the inside.
Find the cost of gravelling the path at ` 2 per m2.
Solution. Area of the plot= (120 × 80)m2 = 9600 m2Area
of the plot (excluding path)= [(120 – 6) × (80 – 6)] m2
(114 × 74) m2 =8436 m2
Area of the path= (9600 – 8436) m2 = 1164 m2
Cost of gravelling the path= ` (1164 × 2) = ` 2328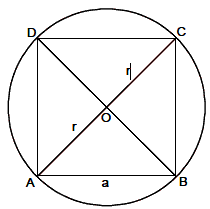
Solution. Solution. Area of the square (side)2= 441m2
Side = 441 = 21 m
Diagonal of a square= Ö2*side = 21Ö
2m
Example 8: Find the area of a square that can be
inscribed in a circle of radius r.
Solution. Let ABCD be a square inscribed in a circle of radius r.
Example 9: Find the area of a triangle whose sides are 6m, 11m and 15m in length.Diagonal AC = 2(OC) = 2r
Let AB = a, then AC =Ö2a
Ö2a = 2r , a = 2/Ö2r = Ö2r
Hence, Area = a2 = ( 2r)2= 2r2
Solution:
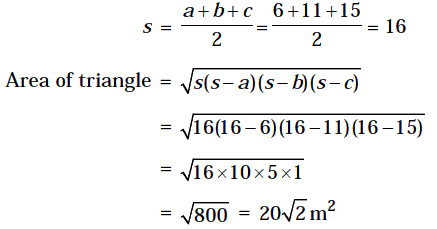
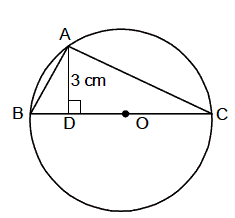
Example 10: Find the area of a right angled triangle which is
inscribed in a circle of radius 4 cmand altitude drawn to the hypotenuse is 3
cm.
Solution.
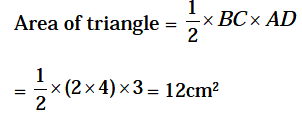
Example 11: Find the percentage increase in the area of a
triangle, if its each side is doubled.
Solution: Let a, b, c be the sides of the given triangle

Example 12: The perimeter of a rhombus is 48 m and the
sum of the lengths of its diagonals is 26 m. Find the area of rhombus.
Solution. The perimeter of rhombus = 4a = 48
Þ a = 12m
If the diagonals of rhombus are d1 and d2, then d1
+ d2 = 26m (given)
Now, by the relation between diagonals and sides of rhombus
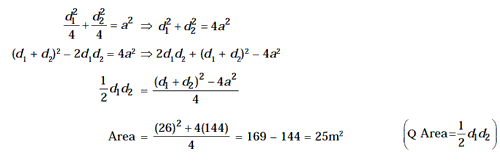
© UPSCPORTAL.COM

