(HOT) UPSC Current Affairs 2025 PDF
NEW! The Gist (NOV-2025) | E-BOOKS
(IGP) IAS Pre Paper - 2: GS - Basic Numeracy - Probability
Basic Numeracy
Probability
Probability
Probability is used to indicate a possibility of an event to occur. It is often used synonymously with chance.
-
In any experiment if the result of an experiment is unique or certain, then the experiment is said to be deterministic in nature.
-
If the result of the experiment is not unique and can be one of the several possible outcomes then the experiment is said to be probabilistic in nature.
Various Terms Used in Defining Probability
-
Random Experiment: Whenever an experiment is conducted any number of times under identical conditions and if the result is not certain and is any one of the several possible outcomes, the experiment is called a trial or a random experiment, the outcomes are known as events. eg, When a die is thrown is a trial, getting a number 1 or 2 or 3 or 4 or 5 or 6 is an event.
-
Equally Likely Events: Events are said to be equally likely when there is no reason to expect any one of them rather than any one of the others. eg, When a die is thrown any number 1 or 2 or 3 or 4 or 5 or 6 may occur. In this trial, the six events are equally likely.
- Exhaustive Events: All the possible events in any trial are known as exhaustive events. eg, When a die is thrown, there are six exhaustive events.
- Mutually Exclusive Events: If the occurrence of any one of the events in a trial prevents the occurrenceof any one of the others, then the events are said to be mutually exclusive events. eg, When a die is thrown the event of getting faces numbered 1 to 6 are mutually exclusive.
Classical Definition of Probability
If in a random experiment, there are n mutually exclusive and equally likely elementary events in which n elementary events are favourable to a particular event E, then the probability of the event E is defined as P (E)
P(E) =Favourabel Events / Total number of Events = n(E ) / n(S) =m/n
If the probability of occurrence of an event E is P(E) and the probability of non-occurrence is P(E) , then,

Addition Theorem on Probability
If El and E2 are two events in a sample space S, then P (El
È E2) = P (El) + P (E2)
– P (El Ç E2). If El
and E2 are mutually exclusive events (disjoint), then
P (El È E2) = P (El)
+ P (E2) . ( P (El Ç E2)
= q)
Independent and Dependent Events
Two or more events are said to be independent if the happening or non-happening of any one does not depend (or not affected) by the happening or non-happening of any other. Otherwise they are called dependent events.
eg, Suppose a card is drawn froma pack of cards and replaced before a second
card is drawn. The result of the second drawn is independent of the first drawn.
If the first card drawn is not replaced, then the second drawn is dependent on
the first drawn. If El and E2 are independent events, then
P (El Ç E2) = P (El
) × P(E2 )
Simple Event
An event which cannot be further split is called a simple event. The set of all simple events in a trial is called a sample space.
Compound Event
When two or more events occur in relation with each other, they are called compound events.
Conditional Event
If El and E2 are events of a sample space S and if E2 occurs after the occurrence of El , then the event of occurrence of E2 after the event E1 is called conditional event of E2 given E1. It is denoted by E2/E1.
Condit ional Probability
If El and E2 are the events in a sample space S and P
(El) ≠ 0, then the probability of
E2 after the event El has occurred is called conditional
probability of E2 given El. It is denoted by P
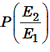
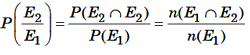
‘Smart’ Facts
- When a die is rolled six events occur. They are {1, 2, 3, 4, 5 and 6}
- When two dice are rolled 36 events occur. They are [(1,1), (1,2), (1,3), (1,4), (1,5), (1,6), (2,1), (2,2), (2,3), (2,4), (2,5), (2,6), (3,1), (3,2), (3,3), (3,4), (3,5), (3,6), (4,1), (4,2), (4,3), (4,4), (4,5), (4,6), (5,1), (5,2), (5,3), (5,4), (5,5), (5,6), (6,1), (6,2), (6,3), (6,4), (6,5), (6,6)]
- When a coin is tossed 2 events occur. They are {H, T}
- When two coins are tossed 4 events occur. They are {HH, HT, TH, T T}
- When three coins are tossed 8 events occur. They are {HHH HHT, HTH, HT T, T HH, THT, T TH, T T T}
- In a pack of 52 cards there are 26 red cards and 26 black cards. The 26 red cards are divided into 13 heart cards and 13 diamond cards. The 26 black cards are divided into 13 club cards and 13 spadecard. Each of the colours, hearts, diamonds, clubs and spades is called a suit. In a suit, we have 13cards (ie, A, K, Q, J, 10, 9, 8, 7, 6, 5, 4, 3 and 2)
Example 1: In a toss of a coin, find the probability of getting a
tail.
Solution. Here, S = [H, T] and E = [T] P(E) = n(E)/n(S
) = 1/2
Example 2: Two unbiased coins are tossed, what is the probability of
getting both heads.
Solution. Here, S = [HH, HT, TH, TT] and E = [HH] P(E) = n(E)/n(S ) = 1/4
Example 3: In a simultaneous throw of a pair of dice, find the
probability of getting a total more than 9.
Solution. Here n(S) = 6 × 6 = 36 Let E = Event of getting a total more
than 9 = [(4, 6), (5, 5), (5, 6), (6, 5), (6, 4), (6, 6)] P(E) = n(E)/n(S ) =
6/36 = 1/6
Example 4: In a simultaneous throw of a pair of dice, find the
probability that the sumof numbers shown on the two faces is divisible by 5 or
6.
Solution. Here, n(S) = 6 × 6 = 36 Let E = Event of getting a sum of
numbers shown on the two faces divisible by 5 or 6. = [(1, 4), (1, 5), (2,
3), (2, 4), (3, 2), (3, 3), (4, 1), (4, 2), (5, 1), (5, 5), (6, 4), (6, 6)]
N(E) = 12
P(E) = n(E)/n(S ) = 12/ 36 = 1/3
Example 5: A card is drawn from a well shuffled pack of cards. Find the probability that it is a (i) queen (ii) a red card (iii) a space. (i) Let E be event of drawing a queen card. Then, one queen card can be drawn from 4 queens in 4C1 ways.
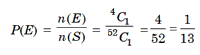
(ii) Let E be the event of drawing a spade card. Then, one spade card can be drawn from13 spade cards in 13C1 ways.
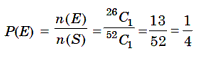
(iii) Let E be the event of drawing a spade card. Then, one spade card can be
drawn from 13 spade cards in 13C1 ways.
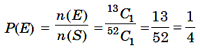

Solution. Out of 52 cards one card can be drawn in 52C1 ways. Let E1 be the event that the card drawn is a diamond, E2 be the event that the card drawn is king and (El ÇE2) be the event that the card drawn is both diamond the king and S be the sample space.
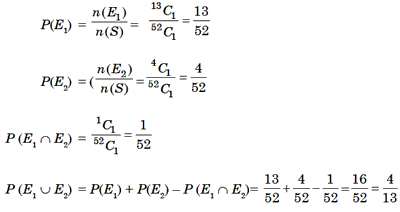
Example 8: A bag contains 4 red balls and 5 white balls. a ball is drawn
at random. Find the probability that it is a red ball or a white ball.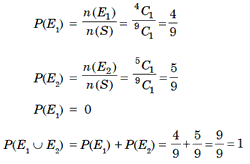
Example 9: A bag contains 4 red balls and 4 white balls. Two balls are
drawn in succession from the bag with replacement, what is the probability that
the two balls are of different colours?
Solution. Let El and E2 denote the events of
drawing balls of different colors in the first and the second draw with
replacement and S be the sample space.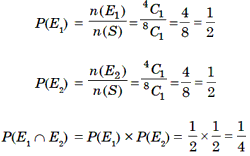
Example 11: In a school, there are 1000 students, out of which
430 are girls. It is known that out of 430, 10% of the girls study in class XII.
What is the probability that a students choosen randomly studies in Class XII
given that the choosen student is a girl?
Solution. Let E denote the event that a student choosen randomly studies
in Class XII and F be the event that the randomly choosen student is a girl. We
have to find P(E|F).
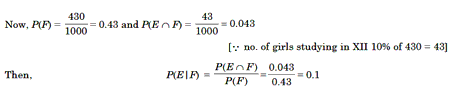
Example 12: A person has undertaken a construction
job. The probabilities are 0.65 that there will be strike, 0.80 that the
construction job will be completed on time if there is no strike, and 0.32 that
the construction job will be completed on time if there is no strike, and 0.32
that the construction job will be completed on time if there is a strike.
Determine that probability that the construction job will be completed on time.
Solution. Let a be the event that the construction job will be completed
on time, and B be the event that there will be a strike. We have to find P(A).
We have
P(B) = 0.65, P(no strike) = P(B') = 1 – P(B) = 1 – 0.65 = 0.35 P(A|B) = 0.32,
P(A|B') = 0.80 Since events B and B¢ form a partition of the sample space S
therefore, by theorem on total probability, we have P(A) = P(B) P(A|B) + P(B')
P(A|B') = 0.65 × 0.32 + 0.35 × 0.8 = 0.208 + 0.28 = 0.488 Thus, the probability
that the construction job will be completed in time is 0.488.
© UPSCPORTAL.COM

