Sets

A set is a collection of well defined objects. The objects of the sets are called elements.

• Sets are usually denoted by capital letters A, B, C,..., X, Y, Z.
• The elements of the sets are denoted by small letters like a, b, c,..., x, y, z etc.

Representation of Sets

Sets are usually described into two ways.

• Tabular form or roster form, in this form, all the elements of the set are separated by commas and enclosed between the bracket { }.

For example
(a) The set of vowels of English Alphabet as A = {a, e, i, o, u)
(b) The set of numbers on a clock face is written as B = (1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12}

(ii) Set builder from: We define a set by stating properties which its elements must satisfy. For example the set of all even integers. Then, we use the letters usually x, and we write A = {x | x is an even integer} This is to be read as A is a set of numbers x such that x is an even integer. The vertical line “ | ” to be read as “such that” some times we use x in place of vertical line.
A = {x : x is an even integer}
eg, C = {1,w, w²} = {x | x³ – 1 = 0} If an object x is an element of a set A, we write x Î A which is read as “x belong to A” and if an object x is not a member of A we write x Ï A and read as “x does not belong to A”.

Some Important Terms

• Empty or Null set The set which contains no elements is called the empty set or the null set. The empty set is written as f.
  Thus, f = { } as there is no element in the empty set.
  For example; the set of odd numbers divisible by 2 is the null set.
• Singleton set A set containing only one element is called a singleton for example, {1}, {4} are singleton sets.
• Equality of sets. The sets A and B are equal if they have same members that is if every elements of A is an element of B and every element of B is an element of A, then A = B eg, if A = { l, 3,5,7} and B = {7, 3, 1, 5}, then A = B If the two sets are not equal we write A ≠ B
  Important Formulae
  1. A set does not change if its elements, are repeated.
  2. A set does not change even if the order of its elements is different.
• Finite and Infinite set. The set which contains a definite number of elements is called a finite set. The set which contains an infinite number of elements is called an infinite set.
  eg, (I) The set of days in a week.
  eg, (II) The set of natural numbers.
• Disjoint set. Two sets A and B are said to be disjoint, if they do not have any element in common. eg, A = { 1, 2, 3}, B = { 4, 5, 6} are disjoint sets.
• Subset. If every element in set A is also an element of another set B. Then A is called a subset of B. Also B is said to be super set of A. Symbolically, we write A Í B (ie, A contained in B) B Í A (ie, B contains A)
  More specifically A Í B if x Î A Þ x Î B eg, (I) Let A = { 2, 4, 7}, B = { 1, 2, 3, 4, 7}
  Then, A Î B since every element of A is in B. eg, (II) A = {x | x a real number} and B = {x | x is an integer} Then, A Ê B
  1. If there is at least one element of A which is not in B, then A is not a subset of B written as A Í B.
  2. Every set is a subset of itself ie, A Í A.
  3. If A Í B and B c Í A, then A = B.
• The Null set f is a subset of every set A.
• Proper Subset: A is a proper subset of B. if A Í B and A ≠ B and is written as A Í B ie, if B contains at least one element more than A, then A is a proper subset of B
• Power set: Set of all the subsets of a set is called the power set eg, A = {a, b, c} subsets of A are f, {a}, {b}, {c}, {a, b}, {b, c}, {c,a}, {a, b, c}
  Hence, P(A) = [f, {a}, {b}, {c}, {a, b}, {b, c}, {c, a}, {a, b, c}] If n is the number of elements of a set A, then the number of subset of A ie, the number of elements of P (A) = 2n.
• Universal set: If all the sets under consideration are the subsets of a fixed set U, then U is called theUniversal set.

Union of sets

Union of two sets A and B is the set of all elements which belongs to A or B (or to both) and is written as A È B (ie, A union B) The same is defined in set builder form as A È B = {x|x Î A or x Î B}

If A = {1, 3, 5, 7, 9} and B = {2, 4, 5, 6, 9} Then, A È B = { 1, 2, 3, 4, 5, 6, 7, 9}

1. From the definition of Union of sets A u B = B u A (Commutative Law) If A is any set, then A È A = A and A È f = A
2. If A and B are any two sets, then A Í (A È B) and B Í (A È B) If x Î A È B,then x Î A or x Î B and if x Ï A È B,then x Î A and x Ï B.
3. If A, B, C are three sets, then A È (B È C) = (A È B) È C

Intersection of Sets

If A and B are any two sets, then intersection of A and B is the set of all elements which are in A and also in B. It is written as A Ç B and is read as “A intersection B’ If A = {2, 4, 6, 8} and B = {4, 5, 6, 9} Then A Ç B = {4, 6}

1. From the definition of the intersection, it follows A Ç B = B Ç A (Commutative Law)
2. If A is any set, then A Ç A = A and A Ç f) = f
3. For any two sets A and B. A Ç B = A and A Ç B Í B
4. If A and B have no elements in common ie, A and B are disjoint, then A Ç B = f If x Î A Ç B = x ÎA and x Î B eg,
   (I) If A = { 2, 3, 6, 8, 9} and B = (1, 3, 5, 6, 7, 9}, then A Ç B = {3, 6, 9}
   (II) If A = {x1|< x < 4 } and B = {x|2 < x < 5}, then A Ç B = {x|2 < x < 4} If A, B, C are three sets, then
   • (A Ç B) Ç C = A Ç (B Ç C) Associative Law
   • A Ç (B Ç C) = (A Ç B) È (A Ç C) Distributive Law

Difference of Sets

The difference of two sets A and B is set of elements which belongs to A but do not belong to B. This is written as A – B A – B = {x| x Î A and x Î B}

1. Set A – B subset of A ie, A – B Î A
2. Set (A – B) and B are disjoint ie, (A – B) Ç B = f
3. A – B = (A È B) – (A Ç B)

Symmetric Difference of Sets

The symmetric difference of two sets A and B is (A – B) È (B – A) and is written as A D B Thus, A D B = (A – B) È (B – A) In the set builder form
A D B = {x | x Î A or x Î B, but x Ï A Ç B}

Demorgan Laws

If A, B, C are three sets, then

• A – (B È C) = (A – B) Ç (A – C)
• A – (B Ç C) = (A – B) È (A – C)

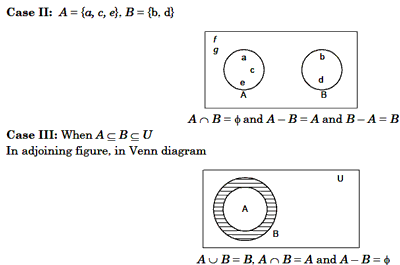
Some resul ts from the Venn diagram
(i) n(A È B) = n (a) + n(B)– n(A Ç B)
(ii) n(A È B) = n (a) + n(B), when A Ç B = F
(iii) n(A – B) + n (A Ç B) = n(A)
(iv) n(B – A) + n (A Ç B) = n(A)
(v) n(A – B) + n (A Ç B) + n (B – A) = n (A Ç B)

Example 1: If in a factory of 30 workers, 10 take tea but not coffee and 14 take tea. Then how many take only coffee ?
Solution. Total number of workers = n (T È C) = 30 Number of workers who take tea n(T) = 14

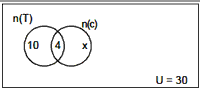
Who take tea but not coffee = n(T – C) = 10
Who drinks both coffee and tea = n (T) – n (T – C) = 14 – 10 = 4
Who takes only coffee = n (C – T) = x
From the figure = x + 4 + 10 = 30 = x = 30 – 14 = 16
The worker who drinks only coffee = 16

Example 2: An elocution competition was held in English and Hindi. Out of 80 students, 45 took part in English, 35 in Hindi, 15 in both English and Hindi, then for the number of students.
(a) Who took part in English but not in Hindi

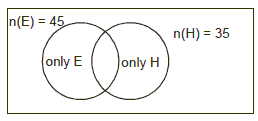
(b) Who took part in Hindi but not in English.
(c) Who took part in either English or Hindi.
(d) Who took part in neither.
Solution. Suppose E is the set of students who took part in English, His the set of students who took part in Hindi, then E n H gives the set of students who took part in both English and Hindi.
(a) The number of students who took part in English but not in Hindi = n(E) = n(E Ç H) = 45 – 15 = 30
(b) The number of students who took part in Hindi but not in English = n(H) – n(E Ç H) = 35 – 15 = 20
(c) The number of students who took part either in English or in Hindi is n(E È H) = n(E) + n(H) – n(E Ç H) = 45 + 35 – 15 = 65
(d) The number of students who took part neither in English nor in Hindi = n (S) –n (T È H) = 80 – 65 = 15

Ordered Pair

If a, b be any two objects, then the pair (a, b) is called the ordered pair. The object a is called the first coordinate (or first number) and b is called the second coordinate (or second number) of the ordered pair (a, b).

1. The ordered pair (a, b) ≠ (b, a) Two ordered pairs (a, b) and (c, d) are said to be equal, if and only if a = c and b = d.

Cartesian Product of Sets

If A and B be any two sets, then Cartesian product of A and B is the set of all ordered pair (a, b), where a Î A and b Î B
Cartesian product of A and B is written as A × B (ie, A cross B) ie A × B = {(a, b) | a Î A and b Î B}

eg, If A = {a, b, c} and B = {1, 2}, then
A × B = {(a, 1), (a, 2),(b, 1),(b, 2),(c, 1),(c, 2)}
B × A = {(1, a),(1, b),(1, c),(2, a),(2, b),(2, c)}
Thus, A × B ¹ B × A
A × A = {(a, a), (a, b), (a, c),(b, a),(b, b),(b, c) (c, a),(c, b),(c, c)}
B × B = {(1, 1), (1, 2),(2, 1),(2, 2))

1. A × (B È C) = (A × B) È (A × C)
2. A ×(B Ç C) = (A × B) È (A × C)

Relations

A relation is a set of ordered pairs. If (x, y) is amember of a relation R, we write it as x R y (ie relation R to y). eg, If R is the ordered pairs of positive integers where R = {(x, y)| x2 = y} The relation is y is a square of x and the set is {(1, 1), (2, 4),(3, 9),(4, 16),...}

Types of Relations

• Reflexive: A relation R on a set A is said to be reflexive for every x Î A (x, x) Î R
• Symmetric Relation: A relation R on a set A is said to be symmetric if x R y Þ y R x (x, y) Î R = (y,x) Î R
  eg, Let A = {1, 2, 3} and R = {(1, 1), (2, 2),(1, 3),(3,1)} Clearly, R is a symmetric relation.
• Transitive Relation: A relation R in a set A is called transitive if x R y and y R z Þ x R z eg, Let R be a relation in the real number defined by “x less than y” then x < y and y < z = x < z
• Equivalence Relation A relation which is reflexive, symmetric and transitive is a equivalence relation.

Functions

If each element of a set A is associated with exactly one element in the set B, then this association is called a function from A to B. The set A is called the domain and the set B is called the co-domain of the function. Consider : A = {1, 2}, and B = (3, 4, 5, 6), then {(1, 4),(2, 5)) is a function {(1, 4),(2, 5),(2, 6)} is not a function since element 2 in the set A have two images 5 and 6 in the set B

1. Each element of A must be associated with exactly one element in the set B.
2. All the elements of the set B need not have the association.
3. The set of elements of B which are associated with the elements of the set A is called the ‘range’ of the function.
4. The range is the subset of the co-domain.

Types of Functions

• One-one Function (injection): A function f : A ® B is said to be a one-one function elements of A have different images in B ie, f(x) = zx, x Î {1, 2, 3}
  f = {(1, 2),(2, 4),(3, 6)}
• Many-one Function: A function f : A ® B is said to be a many-one function if two are n of A have the same images in B.
• Onto Function: A function f : A ® B is called an onto function if every element of B is an image of some elements of A ie, if co-domain = range.
  eg, Let A = {a, b, c, d} and B = {1, 2, 3} f = {(a, 3),(b, 2),(c, 2),(d, 1))
• Into Function: A function f: A –B is called an into function if co-domain ≠ range.

Example 3: A is set of prime numbers less than 20, write A in Roster form.
Solution. Prime numbers Less than 20 are 2, 3, 5, 7, 11; 13, 17, 19 set A in Roster form. A = {2, 3, 5, 7, 11, 13, 17, 19}

Example 4: Let A = {4, 5, 6, 7} and B = {6, 4, 7, 5}, then
Solution. {4, 5, 6, 7} = {6, 4, 7, 5}, since each of the elements 4 , 5, 6, 7 belongs to Band each of the elements 6, 4, 7, 5 belongs to A, then A = B. The set does not change if its elements are rearranged.

Example 5: A = {x² = 16, x is odd}, then
Solution. A is a empty set. x ² = 16 Þ x = + 4 or x = –4, but x is not odd A does not contain any element, A = f

Example 6: Rewrite the following statements using set notations.
(a) x does not belongs to A
(b) A is not a subset of B
(c) H does not include D
(d) d is a member of E.
Solution.
(a) x Ï A
(b) A Ë B
(c) H Ê D
(d) d Î E

Example 7: Let A = {a, b, c}; ie, A contains the elements a, b, c, state whether each of the four statements is correct or incorrect tell why.
(a) a Î A (b) a Î A
(c) {a} Î A (d) {a} Î A
Solution.
(a) a Î A, correct.
(b) Incorrect. The symbol Í must connect two set it indicates that one set a subset of other. Therefore, a Í A is incorrect since a is a member of A, not a subset.
(c) Incorrect. The symbol a connects an objects to a set. It indicates that object is a member of the set. Therefore, {a} Î A is incorrect since {a} is a subset of A.
(d) Correct.

Example 8: If S be the universal set of English alphabet and let A = {a, b, c}, then complement of A is
Solution. AC = {d, e, f … x, y, z}

Example 9: If A = {1, 2, 3, 4} and B = {2, 4, 6, 8}, find A – B, B – A and A D B.
Solution. A – B = {1, 3}, (A – B) contains the elements of A but not the elements of B. Similarly, B – A = 16,81 (B – A) contains the elements of B but not the elements of A. A D B = (A – B) È (B – A) = {1, 3, 6, 8}

© UPSCPORTAL.COM