Unitary method is the basic area of arithmetic. In the CSAT paper this portion of Basic numeracy will help you to solve myriad problems.

Direct Proportion

Two quantities are said to be directly proportional, if on the increase in one the other increases proportionally or on the decrease in one the other decreases proportionally.
eg, More the numbers of articles, More is the cost.
More the number of workers, More is the work done.
Less the number of articles, Less is the cost.
Less the number of workers, Less is the work done.

Indirect Proportion

Two quantities are said to be indirectly proportional, if on the increase in one the other decreases proportionally or on the decrease in one the other increases proportionally.

eg, More the number of workers, less is the number of days required to finish a work. More the speed, less is the time taken to cover a certain distance.

Less the number of workers,more is the number of days required to finish a work. Less the speed, more is the time taken to cover a certain distance.

Chain Rule

When a series of variables are connected with one another, that we know how much of the first kind is equivalent to a given quantity of second, how much of the second is equivalent to a given quantity of the third and so on. The rule by which we can find how much of the last kind is equivalent to a given quantity of the first kind is called the Chain Rule.

Example 1: If 12 apples cost Rs 216, what is the cost of 3 dozen apples ?
Solution. Let the required cost be Rs x. Also, 3 dozen apples = 35 apples more apples, more cost (Direct Proportion);

Apples                                                         Cost in Rs
12                                                                     216
36                                                                        x

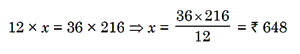
Example 2: A man completes 3/5 of a job in 18 days. At this rate, how many more days will it take him to finish the job?

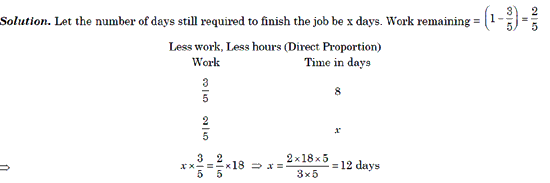
Example 3: A wheel that has 5 cogs is meshed with a larger wheel of 15 cogs. When the smaller wheel has made 27 revolutions, then the number of revolution made by the larger wheel is
Solution. Let the required number of revolutions made by larger wheel be x.
More cogs, Less revolutions (Indirect Proportion)

Cogs                 Revolutions made
5                             27
5                              x

Example 4: If the wages for 8 men for 24 days be Rs 3040, then find the wages of 6 men for 18 days.
Solution. Let the required wages be 7 x.
Less men, Less wages (Direct Proportion)
Less days, Less wages (Direct Proportion)

Men         Days             Wages in Rs
8                24                  3040
6                18                    x

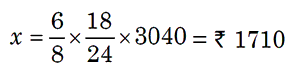
Example 5: If a man walks a certain distance in 20 days when he rests 10 h each day, how long, will it take him to walk three times as far, if he walks twice as fast and rest 12 h each day?
Solution. In the first case the man walks (24 –10)hr = 14h each day. Let the distance travelled bed and the speed be s. In the second case the man walks (24 –12) hr = 12 hr each day. The distance travelled is 3d and the speed is 2 s Let the required number of days be x.

More distance, More days (Direct Proportion)
More speed, Less days (Indirect Proportion)
Less hours, More days (Indirect Proportion)

Distance                 Speed                 Hours Days
d s                             14                         20
3d                              2s                        12 x

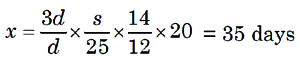
Example 6: A contractor undertakes to complete a road 420 m long in 140 days and employ men for the work. After 70 days he finds that only 140 m of the road is made. How many men should the contractor employ more so that the work may be completed in time?
Solution. In the second case in (140–70) days ie, 70 days the length of the road to be construct (420-140) m ie, 280 m. Let the number of men employed be x.
More length of road, More men (Direct Proportion)

Days         Length of road in metre                 Men
70                     140                                       28
70                     280                                         x

© UPSCPORTAL.COM