(FREE) UPSC Current Affairs 2024 PDF

(Download) UPSC IAS Mains Exam Paper - 2017 : Mathematics

NEW! UPSC MAINS G.S. SOLVED PAPERS (LAST 15 Years)

(Download) UPSC IAS Mains Exam Paper - 2017 : Mathematics

MATHEMATICS
(Paper - 1)

Time Allowed : Three Hours

Maximum Marks : 250

QUESTION PAPER SPECIFIC INSTRUCTIONS

(Please read each of the following instructions carefully before attempting questions)

There are EIGHT questions divided in two Sections and printed both in HINDI and in ENGLISH.

Candidate has to attempt FIVE questions in all.

Question Nos. 1 and 5 are compulsory and out of the remaining, THREE are to be attempted choosing at least ONE question from each Section.

The number of marks carried by each question/part is indicated against it.

Answers must be written in the medium authorized in the Admission Certificate which must be stated clearly on the cover of this Question-cum-Answer (QCA) Booklet in the space provided. No marks will be given for answers written in a medium other than the authorized one.

Assume suitable data, if considered necessary, and indicate the same clearly.

Unless and otherwise indicated, symbols and notations carry their usual standard meanings.

Attempts of questions shall be counted in sequential order. Unless struck off, attempt of a question shall be counted even if attempted partly. Any page or portion of the page left blank in the Question-cum-Answer Booklet must be clearly struck off

SECTION-A

Q1. (a) Let A = (2 2 / 1 3) find a non-singular matrix P such that P^-1 AP is a diagonal martix.
(b) Show that the similar matrices have the same characteristic polynominal.
(c) Intergrate the function F(x,y) = xy (x² + y²) over the domain R: {-3<x²-y²<3, 1<xy<4}.
(d) Find the equation of the tangent pane at point (1,1,1) to the conicoid 3x²-y² = 2z
(e) Find the shortest distance between the skew lines:
x-3/3 = 8-y/1 = z-3/1 and x+3/-3 = y+7/2 = z-6/4.

Q2. (a) Find the volume of the solid above the xy-plane and directly below the portion of the elliptic paraboloid x² + y²/4 = z which is cut off by the plane z=9.
(b) A palne passes through a fixed point (a,b,c) and cut the axis at the points A, B, C respectively. Find the locus of the centre of the sphere which passes through the origin O and A,B,C.
(c) Show that the plane 2x-2y+z+12 = 0 touches the sphere
x²+y²+z²-2x-4y+2z-3 = 0 find the point of contact.
(d) Suppose U and W are distint four dimensional subspaces of a vector space V, where dim V = 6. Find the possible dimensions of subspace U^W.

Q3. (a)

(b) Prove that distinct non-zero eigenvectors of a matrix are linearly independent.

(c)

(d) Find the locus of the point of intersection of three mutually perpendicular tangent planes to ax² + by² + cz² = 1.

Q4. (a) Reduce the following equation to the standard form and hence determine the nature of the conicoid : x²+y²+z²-yz-zx-xy-3x-6y-9z+21 = 0
(b) Consider the following system of equation in x,y,z:

x+2y+2z = 1
x+ay+3z = 3
x+11y+az = b.

(i) For which value of a does the system have a unique solution?
(ii) For which pair of value (a,b) does the system have more than one solution?

SECTION-B

Q5. (a) Find the differential equation representing all the circles in the x-y plane.
(b) Support that the streamlines, of the fluid flow are given by a family of curves xy=c. Find the equipotential lines, that is, the orthogonal trajectories of the family of curves representing the streamlines.
(c) A fixed wire is in the shape of the cardiod r = a (1 + cosq), the initial line being the downward vertical. A small ring of mass m can slide on the wire and is attached to the point r = 0 of the cardiod by an elastic string of natural length a and modulus of elasticity 4 mg. The string is released from rest when the string is horizontal. Show by using the laws of conservation of energy that aq²(1 + cosq)-g cosq (1 - cosq) = 0, g being the acceleration due to gravity.
(d) For what values of the constants a, b and c the vector V = (x +y+az) + (bx +2-z) + (-3+ Cy+2z) k is irrotational. Find the divergence in cylindrical coordinates of this vector with these values.
(e) The position vector of a moving point at time t is r = sinti+cos 2tj+ (t² +2y) k. Find the components of acceleration ā in the directions parallel to the velocity vector ū and perpendicular to the plane of r and ū at time t= 0.

Q6. (a) (i) Solve the following simultaneous linear differential equation:
(D+1)y = z+e^x and (D+1)z = y+e^x where y and z are functions of independent variable x and D = d/dx.
(ii) If the growth rate of the population of bacteria at any time t is proportional to the amount present at that time and population doubles in one week, then how much bacterias can be expected after 4 weeks?

(b) (i) Consider the differential equation xy p² - (x² +y²-1) p +xy = 0 where p=d/dx Substituting u=x² and v = y² reduce the equation to Clairaut's form in terms of u, v and p' = dv/du. Hence, or otherwise solve the equation.
(ii) Solve the following initial value differential equations :
20y" +4y' +y = 0, y(0) = 3.2 and y' (0) = 0.

(c) A uniform solid hemisphere rests on a rough plane inclined to the horizon at an angle f with its curved surface touching the plane. Find the greatest admissible value of the inclination f for equilibrium. If f be less than this value, is the equilibrium stable ?

Q7. (a) Find the curvature vector and its magnitude at any point r = (q) of the curve r= (a cosq, a sinq, aq). Show that the locus of the feet of the perpendicular from the origin to the tangent is a curve that completely lies on the hyperboloid x² + y² - z² = a².
(b) (i) Solve the differential equation:

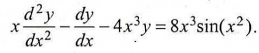
(ii) Solve the Following differential equation using method of variation of parameters:

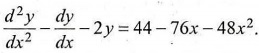
(c) A particle is free to move on a smooth vertical circular wire of radius a. At time t = 0 it is projected along the circle from its lowest point A with velocity just sufficient to carry it to the highest point B. Find the time I at which the reaction between the particle and the wire is zero.

Q8. (a)

(b)

(c)

DOWNLOAD 10 YEARS UPSC MAINS MATHEMATICS OPTIONAL PAPERS PDF

DOWNLOAD UPSC MAINS G.S. (1-4) SOLVED PAPERS PDF

DOWNLOAD UPSC MAINS G.S. 10 Year PAPERS PDF

DOWNLOAD UPSC IAS EXAMS E-BOOKS PDF

Printed Study Material for IAS Mains General Studies

MATHEMATICS
(Paper - 2)

Time Allowed : Three Hours

Maximum Marks : 250

QUESTION PAPER SPECIFIC INSTRUCTIONS

(Please read each of the following instructions carefully before attempting questions)

There are EIGHT questions divided in two Sections and printed both in HINDI and in ENGLISH.

Candidate has to attempt FIVE questions in all.

Question Nos. 1 and 5 are compulsory and out of the remaining, THREE are to be attempted choosing at least ONE question from each Section.

The number of marks carried by each question/part is indicated against it.

Assume suitable data, if considered necessary, and indicate the same clearly.

Unless and otherwise indicated, symbols and notations carry their usual standard meanings.

SECTION-A

Q1. (a) Let x₁ = 2 and x_n+1 = Öxn + 20, n = 1,2,3,... Show that the sequence x₁, x₂, x₃,.... is convergent.
(b) Let G be a group of order n. Show that G is isomorphic to a subgroup of the permutation group S_n:
(c) Find the supremum and the infimum of x/sin x on the interval (0, p/2].
(d) Determine all entire functions f(z) such that 0 is a removable singularity of f(1/z).
(e) Using graphical method, find the maximum value of
2x + y
subject to
4x + 3y < 12
4x + y <8
4x -y <8
x, y > 0.

Q2. (a)

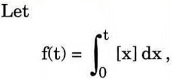
where [x] denotes the largest integer less than or equal to x.
(i) Determine all the real numbers t at which f is differentiable.
(ii) Determine all the real numbers t at which f is continuous but not differentiable.

(b) Using contour integral method, prove that

(c) Let F be a field and F[X] denote the ring of polynomials over F in a single variable X. For f(X), g(X) e F[X] with g(X) = 0, show that there exist q(X), r(X) e F[X] such that degree (r(X)) < degree (g(X)) and f(X) = q(X) • g(X) + r(X).

Q3. (a) Show that the groups Z₅ x Z₇ and Z₃₅ are isomorphic.
(b) Let f = u + iv be an analytic function on the unit disc

(c) Solve the following linear programming problem by simplex method :
Maximize
z = 3x₁ + 5x₂ + 4x₃subject to
2x₁ + 3x₂< 8
2x₂ + 5x₃ < 10
3x₁ + 2x₂ + 4x₃ < 15
x₁, x₂, x₃ > 0.

Q4. (a) For a function f: C → C and n > 1, let f⁽ⁿ⁾ denote the nth derivative off and f⁽⁰⁾ = f. Let f be an entire function such that for some n > 1, f⁽ⁿ⁾ (1/k) = 0 for all k = 1, 2, 3, ..... Show that f is a polynomial.
(b) Find the initial basic feasible solution of the following transportation problem using Vogel's approximation method and find the cost.

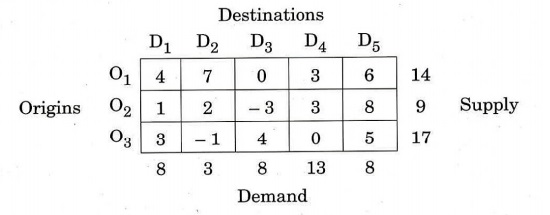
(c)

SECTION-B

Q5. (a) Solve (D² - 2DD' + D'²) z = e^x+2y + x³ + sin2x,
Where

(b) Explain the main steps of the Gauss-Jordan method and apply this method to find the inverse of the matrix

(c) Write the Boolean expression
z (y + z) (x + y + z)
in its simplest form using Boolean postulate rules. Mention the rules used during simplification. Verify your result by constructing the truth table for the given expression and for its simplest form.

(d) Let T be a closed curve in xy-plane and let S denote the region bounded by the curve 1. Let

If f is prescribed at each point (x, y) of S and w is prescribed on the boundary T of S, then prove that any solution w = w(x, y), satisfying these conditions, is unique.

(e) Show that the moment of inertia of an elliptic area of mass M and semi-axis a and b about a semi-diameter of length r is 1/4Ma²b²/r². Further, prove that the moment of inertia about a tangent is 5M/4p², where p is the perpendicular distance from the centre of the ellipse to the tangent.

Q6. (a) Find a complete integral of the partial differential equation
2 (pq + yp + qx) + x² + y²= 0.

(b) For given equidistant values u_₁, u₀, u₁ and u₂, a value is interpolated by Lagrange's formula. Show that it may be written in the form

Where x + y = 1

(c) Two uniform rods AB, AC, each of mass m and length 2a, are smoothly hinged together at A and move on a horizontal plane. At time t, the mass centre of the rods is at the point (€, n) referred to fixed perpendicular axes Ox, Oy in the plane, and the rods make angles q + $ with Ox. Prove that the kinetic energy of the system is

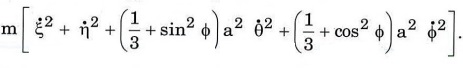
Also derive Lagrange's equations of motion for the system if an external force with components [X, Y] along the axes acts at A.

Q7. (a)

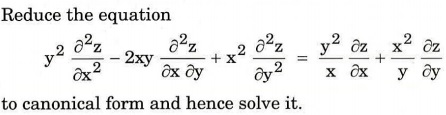
(b)

(c) A stream is rushing from a boiler through a conical pipe, the diameters of the ends of which are D and d. If V and v be the corresponding velocities of the stream and if the motion is assumed to be steady and diverging from the vertex of the cone, then prove that

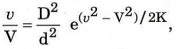
where K is the pressure divided by the density and is constant.

Q8. (a)

(b) Write an algorithm in the form of a flow chart for Newton-Raphson method. Describe the cases of failure of this method.
(c) If the velocity of an incompressible fluid at the point (x, y, z) is given by

then prove that the liquid motion is possible and that the velocity potential is z/r³ Further, determine the streamlines.