(FREE) UPSC Current Affairs 2024 PDF

(Download) UPSC IAS Mains Exam Paper - 2017 : Physics

NEW! UPSC MAINS G.S. SOLVED PAPERS (LAST 15 Years)

(Download) UPSC IAS Mains Exam Paper - 2017 : Physics

PHYSICS
(PAPER-I)

Time Allowed : Three Hours

Maximum Marks : 250

QUESTION PAPER SPECIFIC INSTRUCTIONS

(Please read each of the following instructions carefully before attempting questions)

There are EIGHT questions divided in two Sections and printed both in HINDI and in ENGLISH.

Candidate has to attempt FIVE questions in all.

Question Nos. 1 and 5 are compulsory and out of the remaining, THREE are to be attempted choosing at least ONE question from each Section.

The number of marks carried by each question/part is indicated against it.

Answers must be written in the medium authorized in the Admission Certificate which must be stated clearly on the cover of this Question-cum-Answer (QCA) Booklet in the space provided. No marks will be given for answers written in a medium other than the authorized one.

Assume suitable data, if considered necessary, and indicate the same clearly.

Unless and otherwise indicated, symbols and notations carry their usual standard meanings.

Attempts of questions shall be counted in sequential order. Unless struck off, attempt of a question shall be counted even if attempted partly. Any page or portion of the page left blank in the Question-cum-Answer Booklet must be clearly struck off.

SECTION-A

Q1. (a) Express angular momentum in terms of kinetic, potential and total energy of a satellite of mass m in a circular orbit of radius r.
(b) Describe Michelson-Morley experiment and show how the negative results obtained from this experiment were interpreted.
(c) Sunlight is reflected from a calm lake. The reflected light is 100% polarized at a certain instant. What is the angle between the sun and horizon?
(d) Explain with proper example the interferences due to 'division of wavefront and division of amplitude'.
(e) Find the velocity of sound in a gas in which two waves of wavelengths 1.00 m and 1.01 m produce 10 beats in 3 seconds.

Q2. (a) Define moment of inertia and explain its physical significance. Calculate the moment of inertia of an annular ring about an axis passing through its centre and perpendicular to its plane.
(b) A diatomic molecule can be considered to be made up of two masses m₁ and m₂ separated by a fixed distance r. Derive a formula for the distance of centre of mass, C₁ from mass m₁. Also show that the moment of inertia about an axis through C and perpendicular to r is mr², where m = m₁m₂ / m₁ + m₂.
(c) State and explain Stokes' law. A drop of water of radius 0.01 m is falling through a medium whose density is 1.21 kg/m³ and h =1.8x10^-5 N-s/m². Find the terminal velocity of the drop of water.

Q3. (a) What is multiple-beam interference? Discuss the advantages of multiple-beam interferometry over two-beam interferometry. Explain the fringes formed by Fabry-Perot interferometer.
(b) Show that the areas of all the half-period zones are nearly the same. Find the radius of 1st half-period zone in a zone plate whose focal length is 50 cm and the wavelength of the incident light is 500 nm.
(c) A plane-polarized light passes through a double-refracting crystal of thickness 40 mm and emerges out as circularly polarized. If the birefringence of the crystal is 0.00004, then find the wavelength of the incident light.
(d) Obtain the system matrix for a thin lens placed in air and made of material of refractive index 1.5 having radius of curvature 50 cm each. Also find its focal length.

Q4. (a) A ball moving with a speed of 9 m/s strikes an identical stationary ball such that after the collision the direction of each ball makes an angle 30° with the original line of motion. Find the speed of the balls after the collision. Is the kinetic energy conserved in this collision?
(b) Prove that x² + y² + z²= c²t² is invariant under Lorentz transformation.
(c) How is laser light different from ordinary light? Discuss the working principle of ruby laser. What role do chromium ions play in this process?
(d) Explain the principle of operation of optical fibre. What are the different losses that take place in optical fibre?

SECTION-B

Q5. (a) Discuss the principle of 'artificial dielectric'. Where do you find its use?
(b) How large an inductance needs to be connected in series with a 120 V, 60 W lightbulb if it is to operate normally when the combination is connected across a 240 V, 60 Hz supply?
(c) A charge q = 2 mC is placed at a =10 cm from an infinite grounded conducting plane sheet. Find the (i) total charge induced on the sheet, (ii) force on the charge q and (iii) total work required to remove the charge slowly to an infinite distance from the plane.
(d) 1 litre of hydrogen at 127 °C and 10⁶ dynes/cm² pressure expands isothermally until its volume is doubled and then expands adiabatically until its volume is redoubled. Calculate the resulting pressure. (g = 1.42)
(e) Using the Maxwell-Boltzmann distribution law, show that there cannot be any negative absolute temperature.

Q6. (a) When a person carrying something metallic walks through the doorway of a metal detector, it emits a sound. Explain the reason behind it. A 200 W resistor and a 15 mF capacitor are connected in series to 220 V, 50 Hz a.c. supply. Calculate the current in the circuit and the r.m.s. voltage across the resistor and the capacitor. Is the algebraic sum of these voltages more than the supply voltage? If yes, resolve the paradox.
(b) (i) Write down Stefan-Boltzmann law of radiation and derive it from Planck's law of radiation.
(ii) An aluminium foil of relative emittance 0.1 is placed between two concentric spheres (assumed perfectly black) at temperatures 300 K and 200 K respectively. Find the temperature of the foil once the steady state is reached.
(c) Write down the electromagnetic wave equations in non-conducting dielectric medium. Hence show that the velocity of wave propagation is given by n = Ö1/em, where the symbols have their usual meanings.
(d) A current i(t) = (2e^-t -e^-2t) mA charges up a 120 nF capacitor for a period of 2 seconds. If the final voltage across the capacitor is 15 V, what was the initial voltage across it?

Q7. (a) (i) Why does a soap bubble expand upon electrification?
(ii) A sphere of radius R contains a charge +Q and a charge -Q distributed uniformly in the upper and lower hemispheres respectively. Show that the dipole moment of charge distribution is 3/4 QRk, where k is directed along the polar axis of the spherical coordinate system.
(b) (i) Discuss briefly the features of 'guard rings'.
(ii) The plates of a capacitor are square-shaped, each of side l. The plates are inclined at an angle a to each other. The smallest distance between the plates is a. Calculate the capacitance when a is small.
(c) Write down the physical significance of Maxwell's equations and explain the concept of displacement current by using a proper example.
(d) Derive Clausius-Clapeyron equation. How does it explain the effect of pressure on melting point of solids and boiling point of liquids?

Q8. (a) Write and explain the Maxwell-Boltzmann distribution. Using this distribution, find the expressions for the most probable speed, mean speed and root-mean-square speed.
(b) Calculate the critical temperature for helium, given the values for critical constants, a = 6.15x10^-5, b =9.95x10^-4, where the unit of pressure is atm and the sample is kept at NTP.
(c) A reversible engine converts 1/6 of the heat input into work. When the temperature of the sink is reduced by 62 °C, its efficiency is doubled. Find the temperatures of source and sink.
(d) Explain Bose-Einstein distribution and obtain the same from the grand canonical ensemble.

DOWNLOAD 10 YEARS UPSC MAINS PHYSICS PAPERS PDF

DOWNLOAD UPSC MAINS G.S. (1-4) SOLVED PAPERS PDF

DOWNLOAD UPSC MAINS G.S. 10 Year PAPERS PDF

DOWNLOAD UPSC IAS EXAMS E-BOOKS PDF

UPSC Mains General Studies Study Kit

PHYSICS
(PAPER-II)

Time Allowed : Three Hours

Maximum Marks : 250

QUESTION PAPER SPECIFIC INSTRUCTIONS

(Please read each of the following instructions carefully before attempting questions)

There are EIGHT questions divided in two Sections and printed both in HINDI and in ENGLISH.

Candidate has to attempt FIVE questions in all.

Question Nos. 1 and 5 are compulsory and out of the remaining, THREE are to be attempted choosing at least ONE question from each Section.

The number of marks carried by each question/part is indicated against it.

Assume suitable data, if considered necessary, and indicate the same clearly.

Unless and otherwise indicated, symbols and notations carry their usual standard meanings.

SECTION-A

Q1. (a) A beam of 4.0 keV electrons from a source is incident on a target 50-0 cm away. Find the radius of the electron beamspot due to Heisenberg's uncertainty principle.
(b) Calculate the lowest energy of an electron confined to move in a 1-dimensional potential well of width 10 nm.
(c) Estimate the de Broglie wavelength of the electron orbitting in the first excited state of the hydrogen atom.
(d) Show that the lines in the absorption spectra corresponding to the rotational transitions from two adjacent energy levels of a medium sized molecule at room temperature have comparable intensities.
(e) Given the force constant of HCl molecule = 516 Nm^-1, determine the wave number of the fundamental mode of vibration of the molecule. How many transition lines one can expect in the vibration spectra of HCI molecule at room temperature ?

Q2. (a) Evaluate the most probable distance of the electron from nucleus of a hydrogen atom in its 2p state. What is the probability of finding the electron at this distance ?
(b) Using Schrödinger equation, obtain the eigenfunctions and eigenvalues of energy for a 1-dimensional harmonic oscillator. Sketch the profiles of eigenfunctions for first three energy states.
(c) Calculate the probability of transmission of an electron of 1.0 eV energy through a potential barrier of 4.0 eV and 0.1 nm width.

Q3. (a) Explain Stokes and anti-Stokes Raman scattering with the help of energy level diagram. For a diatomic molecule, obtain expressions for transition energies of its Raman spectra with rotational fine structure and hence the wave numbers of the Stokes lines.
(b) Explain why lines in some Raman spectra are found to be plane polarized to different extents even though the exciting radiation is completely unpolarized ?
(c) State Franck-Condon principle. Define Franck-Condon factors. Using schematic diagram, explain the decay of excited states leading to the phenomena of fluorescence and phosphorescence.

Q4. (a) Explain why the square of the angular momentum (L²) and only one of the components (L_x, L_y, L_z) of L are regarded as constants of motion.
(b) Explain the principle of Nuclear Magnetic Resonance (NMR) with the help of an energy level diagram. Give examples of nuclei which exhibit NMR. What major inferences can be drawn from an NMR spectra ?
(c) In an NMR experiment, hydrogen atoms are subjected to a magnetic field of 5-0 T. Determine the difference in energy (kJ/mol) between two spin states of the nuclei of hydrogen atom and the frequency of radiation required for NMR.

SECTION - B

Q5. (a) Estimate the order of nuclear radius of lead (Z = 82) using the large angle (back) scattering of alpha particles of energy 10 MeV incident on a target (lead).
[Given : (4pe₀,)^-1 = 9x10⁹ Nm²C^-2]
(b) Distinguish between charge independence and charge symmetry of nuclear force. Give one example for each of these.
(c) Describe briefly how parity violation in B-decay was experimentally observed ? What do you understand by the statement, neutrinos are left-handed ?
(d) The energy (E) and wave vector (k) for a conduction band electron in a semiconductor are related as E = ah²k² / m₀ where a is a constant and m₀, is the free electron mass. Calculate the effective mass of the electron.
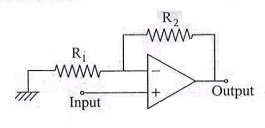
(e) Consider the operational amplifier circuit given above :
Given, R=10 kW, R₂= 150 kW and the product of the open loop gain of the amplifier and its bandwidth = 10⁶ Hz. Determine the closed loop bandwidth of the amplifier.

Q6. (a) (i) Write two properties of deutron which support the existence of non-central tensor force.
(ii) Given that the deutron magnetic moment operator (in units of nuclear magneton) can be expressed as:

(b) (i) How does one explain the approximate constancy of average binding energy per nucleon (BE/A) of nuclei in the region 30<A<170 in the plot of BE/A versus mass number A?
(ii) Write the semi-empirical mass formulla pointing out the role of volume term, surface energy term, coulomb and symmetry energy correction terms.

(c) (i) State the three characteristics properties of stong, weak and electromagnetic forces distinguishing one from the other.
(ii) Point out the interactions in which the following conversation laws are obeyed or violated

(a) Isotopic Spin
(b) Hyper charge
(c) Lepton number
(d) Charge Conjugation

(iii) Write down the Quark constituents of each of the following:

(a) p⁺
(b) K⁺
(c) D⁺⁺
(d) S⁰
(e) W^-

Q7. (a) A system of paramagnetic Atoms (N per unit volume) which can occupy only two energy levels in a uniform ecternal magnetic field H is at a temperature T. If this system follows Boltzman's distribution, find the magnetisation and susceptibility of the system.
(b) Obtain the expression for penetration depth using London's equation of superconductivity and explain its significance.
(c) In a semiconductor, the effective masses of an electron and a hole are 0.07m₀ and 0.4m₀, respectively, where m_o is the free electron mass. Assuming that the average relaxation time for the hole is half of that for the electrons, calculate the mobility of the hole when the mobility of the electrons is 0.8m² volt^-1 s^-1.

Q8. (a) An amplifier in common-emitter configuration is shown in the above figure.
If the current gain b = 100 and the a.c.emiiter resistence = 25.0 W, determine the input impedence and the voltage gain of the amplifier.

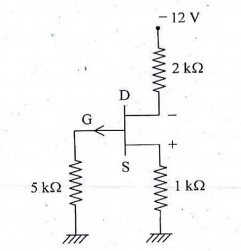
(b) Given above is a current of self biased p-channel JFET.
If the pinch off voltage is 5.0 V and V_DS = 6.0V, Calculate the saturation current I_DSS.

(c) Draw a schematic diagram of the single particle energy levels in a shell model including the effect of spin-orbit coupling. Show how it explains magic numbers in nuclei. Give two examples to show how this scheme predicts the spins and particles of odd A nuclei.